Défi 19

[darkmaster]

Bonjour à tous,
J'ai posté cet exo dans olympiad mais c'est non résolu. Donc je le reposte comme un défi:
On considère les polynômes:
et
soit la racine la plus grande de , soit la racine la plus grande de . Montrer que
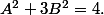
Bonne chance!

[yos]

up!
Pour les pages de brouillon gâchées inutilement, je t'enverrais la facture Dark' .
Z'avez remarqué que ?
Ayant ainsi pulvérisé le record d'inefficacité, je vais me coucher.
Mais il fallait bien faire remonter ce défi.

[Imod]

Ce n'est plus un défi , c'est une horreur !!! Mais je n'avais pas vu ton égalité , yos , je vais "peut-être" m'y remettre .

Imod

[mathelot]

on peut par translation x --->x +k se débarasser du terme en
cette transformation conserve l'ordre des racines.

[yos]

On peut aussi calculer A et B par la méthode de Cardan. Mais ça manque d'élégance.

[darkmaster]

Imaginez que vous avez un concours d'olympiade avec 3 problème pendant 3 heures. Et un des trois est celui-là. :bad3:(Biensûr on a pas le temps pour la méthode de Cardan) Actuellement ce problème a été utilisé dans un concours d'olympiade. Et il est un parmi les plus difficiles que j'ai rencontré.
Généralement, possède 3 racines ; possède 3 racines . On a toujours

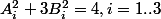
[Yipee]

Es-tu sur de cela Darkmaster. Il me semble (via un tracé sur calculatrice) que les deux polynômes ont deux racines positives. De ce fait je ne vois pas comment peut -être égal à

[darkmaster]

opp je ne suis pas sûr. c'est seulement un souvenir. Je souviens que c'était mon prof qui a dit ça; Et j'ai pas encore vérifié. Je vais te répondre ce soir.

[yos]

Je crois que je le tiens.
En quelques calculs on montre que 3B² et 4-A² sont racines du même poynôme qui doit être . Les 3 égalités s'en déduisent assez facilement.

[darkmaster]

j'ai trouvé l'erreur. Ce doit être et

[yos]

Je détaille un peu.
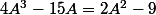
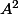
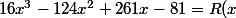De P(A)=0, on tire . En élevant les deux membres au carré, on voit que est racine de . On en déduit que est racine de .
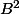
De la même façon est racine de et on en tire est racine de . Ce dernier polynôme est noté U(x).
Les racines de U(x) sont donc mais ce sont aussi (où sont les racines de P et sont celles de Q). D'où l'égalité de ces deux ensembles de racines.
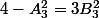
Il reste à prouver que ce qui est facile avec les encadrements des racines par des entiers consécutifs.

[Quidam]

Imaginez que vous avez un concours d'olympiade avec 3 problème pendant 3 heures. Et un des trois est celui-là. :bad3:(Biensûr on a pas le temps pour la méthode de Cardan) Actuellement ce problème a été utilisé dans un concours d'olympiade. Et il est un parmi les plus difficiles que j'ai rencontré.
Généralement, possède 3 racines ; possède 3 racines . On a toujours

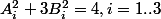
Vérification par programme :
Je trouve effectivement que

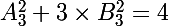
Par contre :



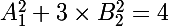
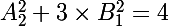
Mais je suis bien incapable de trouver une solution à ce problème difficile !

[darkmaster]

Je détaille un peu.
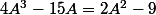
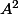
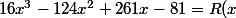De P(A)=0, on tire . En élevant les deux membres au carré, on voit que est racine de . On en déduit que est racine de .
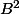
De la même façon est racine de et on en tire est racine de . Ce dernier polynôme est noté U(x).
Les racines de U(x) sont donc mais ce sont aussi (où sont les racines de P et sont celles de Q). D'où l'égalité de ces deux ensembles de racines.
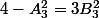
Il reste à prouver que ce qui est facile avec les encadrements des racines par des entiers consécutifs.

Exactement, Yos. C'est une de deux solutions que je connais.Il y a encore une autre mais ta solution est plus naturelle. Par contre, la deuxième est plus jolie et élégante car il éxige pas trop de calcule. On peut essayer le remarque:
Bravo, Yos. Tu mérites le point.La première fois je rencontrais cette exo J'avait perdu 3 journée pour lui mais ça me donne rien. :we:

[yos]

Merci Darkmaster.

[yos]

Pour le défi 20, je passe volontier le relais à Imod qui a résolu un défi bis (sur les moyennes des max-min) il y a peu...