Défi 2

[tize]

Bonjour à tous,

le problème que voici peut se résoudre avec des moyens très simples ! J'ai personnellement mis beaucoup de temps à le résoudre (malgré sa simplicité).
Je le pose pour voir si quelqu'un trouve une solution encore plus simple que la mienne et aussi pour (par la suite) confirmer ma solution par d'autre!
L'énoncé se trouve sur un site très célèbre, je mets un lien ici :ptdr:

[fahr451]

ouaff ouaff :)
site très célèbre et problème historiquement posé par un intervenant également très célèbre.

[Imod]

Je n'avais même pas essayé tant ce problème m'en rappelait d'autres soit triviaux ou alors carrément encore ouverts mais après quelques essais celui-ci semble intéressant .

J'y regarde de plus près ...

Imod

[yos]

Vive le recyclage.
J'ai pas trop d'idée.
Si on fait un pavage du plan par des triangles équilatéraux de côté 1, on a naturellement des triangles équilatéraux de côté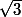 . Si ABC est l'un des triangles de côté 1, on lui met A et B en rouge et C en vert. On est alors obligé de mettre tous les sommets situés sur (AB) en rouge et tous ceux sur la parallèle à (AB) passant par C en vert (sinon un triangle unicolore apparait). Il en va de même des autres parallèles à (AB) : alternance de droites vertes et rouges.
Mais dans ce réseau, je ne vois pas d'unicolore.

[maturin]

donc le réseau de yos est un ensemble des droite verticales avec:
toutes les droites avec n+p impair sont vertes.
tous les droites avec n'+p' pair sont rouges.

et moi je vois pas d'impossibilité là dedans...

[maturin]

le problème c'est que tu peux effectivement constuire un réseau de droite parallèle qui t'empèchera d'avoir des triangles ayant une de leur base soit parallèle soit orthogonale à ce réseau.

Mais si tu fais une petite rotation de moins de pi/2 ça te fera un autre réseau de droites parallèles...

[Imod]

En raisonnant par l'absurde , le maillage proposé par yos est le seul possible ne fournissant pas de triangles équilatéraux unicolores dont les sommets sont aux noeuds du maillage . On remarquera que tout segment du maillage de longueur 2 a ses extrémités unicolores . En considérant l'ensemble des droites passant par un point donné on obtient un cercle de la couleur du centre et de rayon 2 donc tout cercle de rayon 2 est de la couleur de son centre . Ceci me semble aberrant .

Imod

[tize]

Bravo Imod ! :++:
Pour le démontrer j'avais utilisé presque la même méthode que toi : avec des cercles de rayons 2 mais sans passer par les maillages, on peut faire un raisonnement direct :
Si vert (V) est au centre du cercle alors pour tout point (sommet) rouge (R) du cercle, l'un des deux autres sommets du triangle de côté inscrit dans le cercle est V (sinon triangle équilatéral unicolore R de côté ). Du coup étant donné que le centre est V et que l'on a un autre point V (bien placé-faire un dessin) on a nécessairement le point diamétralement opposé à R qui est aussi R. Conclusion : comme il n'y a que deux couleurs, les points diamétralement opposés à un R(resp. V) sont R (resp. V) et la couleur du centre n'a en fait pas d'importance ! De là on peut construire des cercles unicolore de rayon 2...
A ton tour de poser une question Imod et encore Bravo !

[Imod]

Je vais me plier aux règles du jeu ,

je ne suis pas très doué pour inventer des problèmes mais en voici un original auquel j'ai pu apporter une solution :
Des fourmis circulent sur un cercle , toutes à la même vitesse mais pas toutes dans le même sens , à chaque rencontre les fourmis changent de sens de parcours en conservant la même vitesse . Le phénomène a-t-il un caractère turbulent ou périodique ? S'il est périodique quelle est la période ?

Imod

[Yipee]

On suppose qu'il y a un nombre finis de fourmis ?

[Imod]

Oui les fourmis sont en nombre fini on peut même dire qu'il y en a p qui tournent dans un sens et q dans l'autre , p et q sont constants car à chaque rencontre les deux fourmis changent de sens .

Imod

[Flodelarab]

Ne serait ce pas le principe du jeu de morpion ?

On fait des croix, des maillages, jusqu'a déborder l'autre.

[BQss]

En tout cas on se rend compte qu'il y a une periode en faisant une simulation pour un petit nombre. Il arrive un moment ou tout le monde revient au meme endroit en se deplacant dans le sens initiale.
Pour le prouver mathematiquement, je pense qu'il faut le faire par reccurence, on le montre pour 2 ou 3 fourmis pour inicier la recurrence et on le deduit pour n fourmis en supposant que si pour n fourmis il y a une periode alors il y en aura une pour n+1 fourmis.

*C'est l'idée de ta demo IMOD?

Par exemple soit T le temps tel que (u1*(t+T),u2*(t+T),...,un(t+T))=(u1*(t),u2*(t),...,un(t))
avec ui la position de la ième fourmi (i arbitrairement choisi) au temps t et * indiquant que la fourmi avance dans le sens trigonometrique.

Montrons alors que [(u1*(t+T'),u2*(t+T'),...,un(t+T')),(un+1(t+T'))]=(u1*(t),u2*(t),...,un(t)),(un+1(t))] pour un certains T' avec T'=T+C et C une constante de temps relatif au decalage resultant du rajout d'une fourmi dans la chaine.

Bon maintenant il faut le prouver :P.

[Imod]

BQss ,

l'idée de ma démonstration est bien plus simple mais avant d'y penser j'en ai eu d'autres bien pire que la tienne . Je dévoile quand même l'étincelle qui m'a rendu le problème évident , on pourrait très bien considérer que les fourmis qui se heurtent ne changent pas de direction mais échangent seulement leurs passeports avec les fourmis qu'elles ont heurtées et poursuivent leur chemin . Le problème se ramène donc au suivi des passeports dans une ronde de fourmi parfaitement régulière .

J'espère n'en avoir pas trop dit

Imod

[tize]

BQss ,

l'idée de ma démonstration est bien plus simple mais avant d'y penser j'en ai eu d'autres bien pire que la tienne . Je dévoile quand même l'étincelle qui m'a rendu le problème évident , on pourrait très bien considérer que les fourmis qui se heurtent ne changent pas de direction mais échangent seulement leurs passeports avec les fourmis qu'elles ont heurtées et poursuivent leur chemin . Le problème se ramène donc au suivi des passeports dans une ronde de fourmi parfaitement régulière .

J'espère n'en avoir pas trop dit

Imod

Très belle idée !

[BQss]

BQss ,

l'idée de ma démonstration est bien plus simple mais avant d'y penser j'en ai eu d'autres bien pire que la tienne . Je dévoile quand même l'étincelle qui m'a rendu le problème évident , on pourrait très bien considérer que les fourmis qui se heurtent ne changent pas de direction mais échangent seulement leurs passeports avec les fourmis qu'elles ont heurtées et poursuivent leur chemin . Le problème se ramène donc au suivi des passeports dans une ronde de fourmi parfaitement régulière .

J'espère n'en avoir pas trop dit

Imod

Tres joli, il reste alors a prouver que chacune retrouve son passeport simultanement, si en plus il y a meme un moment ou elles le retrouvent au meme endroit (un multiple de la periode que j'appelle temporelle)il y aura aussi une periode a caractere spatiale, est ce qu'elles coincident(ces periodes) ou il y a un nombre de tours k necessaires pour que les fourmis retrouvent toute la meme trajectoires exactement au meme endroit ?

Le truc c'est que si on ne differencie pas les fourmis, c'est clairement periodique, vu que si on considere les differentes trajectoires ui(t) d'une fourmi qui ne changerait pas de chemin en partant de sa position u0, cette fonction passe de fourmi en fourmi et a chaque instant une fourmi quelquonque k est porteuse de cette trajectoire.

Il suffit donc que cette trajectoire parcours un tour entier et on retrouvera au meme endroit une fourmi porteuse. Chaque passeport se retrouvera a la meme place, mais pas forcement porté par la meme fourmi. Le fait que la vitesse soit constante fait que chaque trajectoire a parcouru la meme chemin au bout du meme temps, prendre une distance d'un tour assure le fait qu'il y aura une fourmi porteuse au meme endroit.
Donc en fait au bout d'un temps t=2PiR/v on retrouve la meme disposition, vu qu'on retrouve forcement un passeport et donc une fourmi au meme endroit, le passeport virtuel aura fait un tour et il y aura une fourmi k quelquonque a chaque endroit ou il y en avait une t=2PiR/v avant...

Le caractere de la trajectoire assure que la fourmi porteuse un tour plus tard au meme endroit aura evidemment le meme sens de deplacement que la fourmi qui se trouvait a la meme place un tour plutot vu que c'est la trajectoire et pas la fourmi qu'on a choisi comme critere, une nouvelle fois on ne sait juste pas quelle fourmi porte cette trajectoire.

[BQss]

Mais en rajoutant le fait que les fourmis sont toujours placées dans le meme ordre, vu qu'elles sont coincées entre deux autres et rebondissent entre celles qui l'entourent, il suffit de voir s'il y a un temps T'=kT=k * 2PIR/v au bout du quel une fourmi reference sera au meme endroit, c'est a dire au bout d'un certain nombre de tour virtuel parcourus par la fourmi imaginaire qui ne s'arrete jamais.

Comme on sait que toutes les autres fourmis occuperont toutes un endroit occupé par une autre un tour avant a un temps multiple de 2PIR/v, mais que par ailleurs on sait qu'elles sont classées dans le meme ordre sur le cercle, alors si une et une seule se retrouvent a la meme position à 2kPIR/v, toutes les autres par voix de consequences se retrouveront egalement a la meme position, elles seront alors forcement elles meme porteuses de leur propre trajectoire au meme endroit(si une fourmi i se retrouvent au meme endroit a un multiple de 2PIr/v alors la suivante i+1 qui se retrouvera porteuse de la trajectoire de sa suivante a l'epoque portera aussi la trajectoire de sa suivante de l'epoque (a 2piR/V on retrouve la meme configuration), or sa suivante est toujours la meme, donc sa suivante porte egalement sa propre trajectoire)...

[BQss]

Soit i une fourmi se trouvant au meme endroit que cette fourmi de reference a t0+2kPIR/v donc.

Soit c'est la meme et alors on a une periode de 2kPIR/v car evidemment si c'est la meme fourmi au meme endroit toutes les autres comme je l'ai indiqué plus haut le seront aussi(car elles sont dans le meme ordre sur le cercle) et l'on se retrouve dans les meme conditions qu'au depart et donc a nouveau apres un temps T=2kPIR/v la meme configuration avec les memes fourmis se representera vu que les conditions reste identique (vitesse constante).

Soit alors cette fourmi est differente, mais alors c'est que le phenomene s'est transmis entre la fourmi de reference et cette ième fourmi, cependant chaque fourmi occupant alors la place d'une autre un tour virtuel avant(à t0=t-2PIR/v, d'apres ce que j'ai dit avant), le phenomene va se reproduire a l'identique avec les fourmis a des nouvelles places, et en particulier avec la ième fourmi a la place de reference(celle qui nous interesse) soit a1,a2,...an l'ordre permanent dans lequel les fourmis sont rangés (disons le sens trigo) soit alors k le nombre de rang que la nouvelle fourmi i a avancé pour occuper la position de la fourmi de reference(par voix de consequence toute les fourmis ont alors avancés de k dans la chaine et se retrouve k rang plus loin a t=to+2PIR/V) .

Ce nombre k est alors clairement la periode a laquelle avance la chaine du phenomene a chaque t=2PIR/v vu que l'on repart de la meme configuration(avec toute les fourmis qui ont avancé de k) a chaque 2PIR/v.

Tout les tours le phenomene avance de k fourmis. Il suffit maintenant de montrer que forcement k coincide alors avec la n+1ieme=1ere fourmi au bout d'un certain nombre de tour p, c'est a dire que le phenomene a avancé d'un multiple de n rang.

On a p*k le nombre de rang qui ont été parcouru par la chaine de fourmi au bout de p tour(par la fourmi qui ne s'arrete jamais) et m*n un multiple de n admissible indiquant qu'on coincide bien avec la premiere fourmi de reference(c'est a dire que toute les fourmis retrouvent leur place en meme temps par la meme occasion).

Le probleme revient donc maintenant a demontrer que quelque soit k<=n un couple d'entier il existe p et m couple d'entier tel que:

p*k=m*n=PPCM(k,n) avec k et n fixé k<=n.
Ce qui est evidemment le cas il suffit de poser p=PPCM(k,n)/k et m=PPCM(k,n)/n (m,n) etant inferieur à n.
-On aura p=n et m=k si k et n sont premiers entre eux.
- et si n est divisible par k il ne sera pas necessaire d'attendre autant et la periode sera simplement de p=PPCM(n,k)/k=n/k tour)

On aura donc au bout de p=PPCM(k,n)/k tour (n etant le nombre de fourmis, k la periode d'avancé d ela chaine) ou meme n/k tour si k divise n et de toute facon au bout de n tour dans tout les cas coincidé avec la 1ere fourmi de reference(on aura alors parcouru k(le nombre de rang parcouru a chaque tour) fois le nombre totale de fourmis dans le cas ou n et k sont premiers entre eux par exemple) .


Cette fourmi se retrouve donc alors a la meme place qu'elle etait n tours (au pire) virtuel(parcouru par la fourmi qui ne s'arrete jamais) avant. Toute les autres se retrouvent alors egalement a la meme place d'apres ce que j'ai dit dans le precedent post et alors le phenomene peut recommencer evidemment au bout du meme temps on aura a nouveau la meme configuration.


Finalement oui le phenomene est periodique de plus petite periode T = 2PIr/v * PPCM(n,k)/k avec r le rayon du cercle, v la vitesse des fourmis , n le nombre de fourmis et k la periode d'avancée de la chaine. Il est meme de periode n/k*2PIR/v si k est un diviseur de n avec k la periode d'avancé de la chaine tout les t=2PIr/v. Au pire dans le cas ou k ne divise pas n la periode vaut T=2PIr/v * n et depend exclusivement du nombre de fourmis

[Imod]

Beau travail BQss , mais ce n'est pas fini :fire2: . Ce qui n'est pas facile dans ce problème c'est de trouver la bonne représentation et les bons paramètres . Le terme de période prête à confusion , l'interprétation la plus simple on prend comme unité de temps le tour ( pour une fourmi tournant seule sur le cercle ) . La question est donc ( pour l'interprétation avec les passeports ) après combien de tours chaque fourmi aura retrouvé sa place et son passeport . La réponse dépend uniquement du nombre de fourmis tournant dans chaque sens elle ne dépend donc pas de la position initiale des fourmis .
Une modélisation possible du problème : il y a deux types de fourmis les rouges qui tournent dans le sens direct et les noires qui tournent dans le sens rétrograde . On a en fait deux anneaux de fourmis qui tournent à la même vitesse mais dans le sens contraire . On peut noter :
R ={0+;1+;...;(p-1)+} l'ensemble des fourmis rouges
N={0-;1-;...;(q-1)-} l'ensemble des fourmis noires

Pour mieux voir les choses , on peut considérer un repère lié à N alors seules les fourmis rouges se déplacent ( deux fois plus vite ) . Il n'y a plus qu'à essayer de suivre le passeport de 0+ .



Imod

[BQss]

La question est donc ( pour l'interprétation avec les passeports ) après combien de tours chaque fourmi aura retrouvé sa place et son passeport . La réponse dépend uniquement du nombre de fourmis tournant dans chaque sens elle ne dépend donc pas de la position initiale des fourmis .

Meme si ce n'est pas la plus petite periode en generale, j'ai demontré que au bout de n "tour" (avec n le nombre de fourmis) chaque fourmis retrouvait sa position initiale dans tout les cas.
J'ai donc trouvé une periode valable T=2piR/v * n = (nb de tour) * n , du phenomene .

Dans le cas general c'est vrai que je n'ai pas dit ce que vallait k l'avancement de la chaine tout les tours mais juste prouvé qu'il y en avait un et que au bout de PPCM(k,n)/k tours les fourmis retrouvaient leur position initiale.