Défi à tiroirs
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 10 Juil 2007, 22:01
par Imod » 10 Juil 2007, 22:01
Un défi qui a déjà été proposé à plusieurs reprises sur ce site et sur d'autres , je n'ai toujours pas vu de solution simple . Je vous invite donc à le lever ici bribes par bribes ( il faut répondre aux questions et si possible deviner le défi visé ) .
On dira qu'une suite
)
à éléments rationnels converge vers 0 modulo 1 s'il existe une suite
)
à valeurs entières telle que la suite
)
converge vers 0 ( usuellement ) .
1°) Quelles sont les valeurs
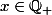
pour lesquelles la suite

converge vers 0 modulo 1 ?
Bon courage !!!
Imod

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 10 Juil 2007, 22:55
par nuage » 10 Juil 2007, 22:55
Salut,
ça n'a pas l'air évident.
Enfin je peux donner deux exemples :
Les rationnels entre 0 et 1. (C'est trivial)
Et
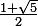
(par référence à Fibbonaci).
Je me demande d'ailleurs si les suites récurrentes ne sont pas une piste importante.
Enfin je regarderai plus précisément demain.
[modification] il faudra bien, qu'un jour, j'apprenne à lire :marteau:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 11 Juil 2007, 01:13
par tize » 11 Juil 2007, 01:13
Bonjour,
les nombres recherchés sont des nombres de Pisot (voir
ici par exemple...).
L'implication :

est un nombre de pisot =>

tend vers 0 dans
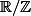
est assez facile à montrer, dans l'autre sens je ne sais pas faire...
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 11 Juil 2007, 07:00
par alben » 11 Juil 2007, 07:00
Bonjour,
Si j'ai bien compris le problème, tout rationnel compris entre 0 et 1 satisfait la condition en prenant pour u la suite nulle. De même pour les entiers avec (u) =(x)
Il reste le cas x=p/q avec p>q et je pense que l'on peut prendre u=partie entière de x sans nuire à la généralité.
Il resterait donc à qualifier des rationnels >1 tels qu'à partir d'un certain rang, la partie fractionnaire de leurs puissances soit décroissante. Il me semble que c'est impossible
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 11 Juil 2007, 09:45
par cesar » 11 Juil 2007, 09:45
vous avez oublié de citer le cas trivial : x entier, tous les entiers naturels verifient la convergence vers 0....
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Juil 2007, 09:45
par yos » 11 Juil 2007, 09:45
Bonjour.
C'est le fait de se limiter à Q+ qui doit nécessiter une approche différente. Sans doute plus simple.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 11 Juil 2007, 09:48
par Imod » 11 Juil 2007, 09:48
Rien à ajouter pour le moment , vous êtes sur la bonne voie :we:
Imod
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 11 Juil 2007, 13:14
par cesar » 11 Juil 2007, 13:14
il faut trouver x = p/q >0 tel que lim (
^n)
-E(
^n)
))=0 lorsque n tend vers l'infini, soit
si on pose :
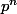
mod
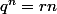
on doit avoir lim (
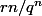
) = 0
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 11 Juil 2007, 13:15
par BiZi » 11 Juil 2007, 13:15
cesar a écrit:il trouver x = p/q >0 tel que lim (
^n)
-E(
^n)
))=0 lorsque n tend vers l'infini
Sans blague :ptdr:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 11 Juil 2007, 13:29
par Imod » 11 Juil 2007, 13:29
cesar a écrit:il faut trouver x = p/q >0 tel que lim (
^n)
-E(
^n)
))=0 lorsque n tend vers l'infini
Pourquoi la limite ne peut-elle pas être égale à 1 ?
Imod
-
achille
- Membre Naturel
- Messages: 94
- Enregistré le: 27 Juin 2007, 11:21
-
 par achille » 11 Juil 2007, 13:35
par achille » 11 Juil 2007, 13:35
en effet hier avant de dormir j'avais vu votre exo, et j'ai eu l'intuition de choisir la suite des entiers par les puissances de la partie entière d x, je pense plutôt qui faut faire l'écriture x = p + r tq p c'est la partie entière et r [0.1[, puis par binôme de Newton x^n -p^n = sum(k=1...n) C(k_n)p^(n-k)r^k , mais allez vous casser la tête avec ce monstre à démontrer qu'il est de limite nulle pour n tend vers l'infini...
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 11 Juil 2007, 13:45
par Imod » 11 Juil 2007, 13:45
Pour les rationnels
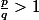
, et non entiers , il me semble plus judicieux d'utiliser la division euclidienne plutôt que la décomposition en partie entière et partie décimale . Je n'en dis pas plus :scotch:
Imod
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 11 Juil 2007, 13:53
par BiZi » 11 Juil 2007, 13:53
achille a écrit:en effet hier avant de dormir j'avais vu votre exo, et j'ai eu l'intuition de choisir la suite des entiers par les puissances de la partie entière d x, je pense plutôt qui faut faire l'écriture x = p + r tq p c'est la partie entière et r [0.1[, puis par binôme de Newton x^n -p^n = sum(k=1...n) C(k_n)p^(n-k)r^k , mais allez vous casser la tête avec ce monstre à démontrer qu'il est de limite nulle pour n tend vers l'infini...
J'ai fait un peu pareil; en fait, j'ai plutôt raisonné par l'absurde (parce que en regardant ma calculette j'ai trouvé aucun rationnel positif q tel que
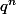
converge vers 0 modulo 1). Donc en écrivant la division euclidienne de
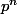
par
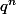
:
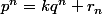
avec
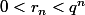
. Puis j'ai élevé au carré, soit
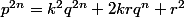
Le but était d'exprimer
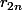
en fonction de
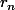
et d'essayer d'aboutir à une contradiction (par exemple que dès que

devient trop petit,
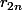
devient grand. Mais malheureusement, affirmer que
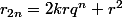
me semble très contestable.... Et élever
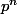
à une puissance supérieure avec le binôme de Newton devient vite affreux!
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 12 Juil 2007, 23:11
par Imod » 12 Juil 2007, 23:11
Demain je donne un indice , un problème à tiroir qui coince sur la première marche , ça manque de sérieux !
Imod

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 13 Juil 2007, 00:11
par nuage » 13 Juil 2007, 00:11
Salut,
juste une idée comme ça.
En posant
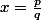
, avec p et q premiers entre eux, on peut regarder le développement de

en base q.
Je ne sais pas si ça donne quelque chose, mais la période est q-1 ce qui semble empêcher la convergence vers zéro de la partie fractionnaire.
C'est un argument insuffisant dans la mesure où le développement à une partie irrégulière.
Mais peut-être une piste... :mur:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 13 Juil 2007, 09:16
par Imod » 13 Juil 2007, 09:16
Un indice pour le cas
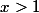
:
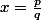
irréductible avec
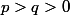
. On suppose que

converge vers 0 modulo 1 , c'est à dire qu'il existe une suite

d'entiers telle que :
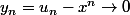
. Que dire alors de la suite
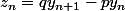
?
Imod
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 13 Juil 2007, 10:16
par emdro » 13 Juil 2007, 10:16
Bonjour,
je découvre cette nouvelle énigme, j'espère ne pas arriver comme un cheveu sur la soupe...
Ta suite z ainsi définie est une suite d'entiers (il suffit de l'écrire) qui tend vers 0. Elle est donc stationnaire nulle à partir d'un moment.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 13 Juil 2007, 10:23
par Imod » 13 Juil 2007, 10:23
emdro a écrit:Ta suite z ainsi définie est une suite d'entiers (il suffit de l'écrire) qui tend vers 0. Elle est donc stationnaire nulle à partir d'un moment.
Oui et maintenant il faut conclure : quelle conséquence pour

?
Imod
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 13 Juil 2007, 10:38
par emdro » 13 Juil 2007, 10:38
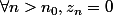
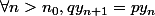
=p(u_n-x^n))
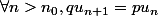
Et donc pour k entier,
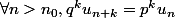
Cela prouve que
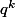
divise

(Gauss).
Et comme c'est vrai pour tout k, c'est absurde si on n'a pas q=1 [car

n'est pas nul (car on a supposé x>1)].
Il n'y a donc pas de nombres rationnels [non entier] supérieurs à 1 dont les puissances tendent vers 0 modulo 1.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 13 Juil 2007, 10:49
par Imod » 13 Juil 2007, 10:49
Pour conclure , les seuls rationnels positifs dont la suite des puissances nième converge modulo 1 sont les rationnels inférieurs à 1 et les entiers . Deuxième tiroir :
2°) Soient

des rationnel non nuls et
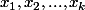
des rationnels positifs distincts . A quelle condition
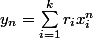
converge-t-elle vers 0 modulo 1 ?
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités