Défi 18
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Jan 2007, 13:16
par yos » 07 Jan 2007, 13:16
C'est pas de l'arithmétique aviateurpilote, mais cela devrait te convenir. J'en ai un beau en arithmétique, mais il faut que je vérifie plusieurs points, alors en attendant le défi 18 pourrait être :
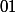
.
-
MikO
- Membre Relatif
- Messages: 106
- Enregistré le: 27 Nov 2006, 19:21
-
 par MikO » 07 Jan 2007, 13:22
par MikO » 07 Jan 2007, 13:22
Yos on la deja traité ce sujet, c'est un exo du cg :) dailleurs ca avait foutu un beau bordell ...
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 07 Jan 2007, 14:50
par darkmaster » 07 Jan 2007, 14:50
Bonjour, Yos,

On doit montrer que

On a
^{xy})
Par l'étude de la fonction
=x^x)
sur
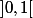
on a

-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 07 Jan 2007, 17:14
par alben » 07 Jan 2007, 17:14
darkmaster a écrit:On a
^{xy})
Bonsoir,
quelque chose m'échappe :
^{x+y})
D'ailleurs

n'est pas vrai : x=0,1 et y=0,8->0,155
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 07 Jan 2007, 17:18
par Imod » 07 Jan 2007, 17:18
darkmaster a écrit:On a
^{xy})
Peux-tu expliquer ? Je n'ai pas dû comprendre ta manip , j'arrive à :
^{x+y})
.
Merci d'avance .
Imod
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Jan 2007, 17:59
par yos » 07 Jan 2007, 17:59
MikO a écrit:Yos on la deja traité ce sujet, c'est un exo du cg

dailleurs ca avait foutu un beau bordell ...
Ca fait longtemps alors?
Et le bordell était dû à l'exo ou bien à certains forumeurs?
-
MikO
- Membre Relatif
- Messages: 106
- Enregistré le: 27 Nov 2006, 19:21
-
 par MikO » 07 Jan 2007, 20:10
par MikO » 07 Jan 2007, 20:10
:D ca a bel et bien été proposé il ya un an, quand o bordel jai confondu avec le thread concernant lequatioin x^y=y^x ( mémorable ! )
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 07 Jan 2007, 20:25
par darkmaster » 07 Jan 2007, 20:25
Imod a écrit:Peux-tu expliquer ? Je n'ai pas dû comprendre ta manip , j'arrive à :
^{x+y})
.
Merci d'avance .
Imod
ah oui, je suis trompé. :briques: :marteau: :marteau: :marteau:
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 07 Jan 2007, 22:27
par alben » 07 Jan 2007, 22:27
Une idée :
On considère la fonction h : ]0,1]-->R telle que
=\frac{Ln(x)}{x-1})
Elle est décroissante et donc

et y>x aussi donc ln(y)+1 >0 et
y^x+y y^{x-1}=(Ln(y)+1)(y^x)\geq 0)
La fonction est donc croissante en x et pour tout y fixé, sa valeur mini sera f(1/e,y)
Il reste à montrer que c'est toujours supérieur à 1
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Jan 2007, 22:51
par yos » 07 Jan 2007, 22:51
Pour le second cas, il faudrait pas regarder

?
Mais j'ai regardé assez vite.
En tout cas ça me parait très bien.
Ah je vois que tu as modifié.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 07 Jan 2007, 23:19
par alben » 07 Jan 2007, 23:19
Oui, la fin était un peu vaseuse. En fait, on peut se ramener au cas 1, l'inégalité
x^y+x x^{y-1}=(Ln(x)+1)(x^y))
reste vraie et comme Ln(x)+1 =0, la fonction de y f(1/e,y) est décroissante et son mini est finalement f(1/e,1)=1+1/e >1
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 07 Jan 2007, 23:44
par darkmaster » 07 Jan 2007, 23:44
J'ai dit que je déteste l'étude de fonction:
L'inégalité arithmético-géométrique(IAG): 
avec
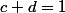
En utilisant cette inégalité;
On a
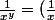^y1^{1-y} \leq \frac{y}{x}+1-y \Rightarrow x^y\geq \frac{x}{x+y-xy})
Et

. En ajoutant

-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 08 Jan 2007, 05:44
par alben » 08 Jan 2007, 05:44
Bravo Darkmaster !
C'est moins fastidieux.
A toi la main :we:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Jan 2007, 07:26
par yos » 08 Jan 2007, 07:26
Bravo Darkmaster. Belle preuve.
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 08 Jan 2007, 12:15
par darkmaster » 08 Jan 2007, 12:15
:girl2: :girl2: :girl2: :girl2: :girl2: merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
 .
.