Saiga a écrit:J'ai peut-être une piste.
Mais il faut déjà que je démontre que pour
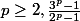
n'est pas un entier, histoire de pouvoir ensuite travailler sur des inégalités strictes.
A suivre...
Je pense avoir trouvé une preuve de ce résultat mais elle est un peu technique. L'idée est de supposer que
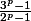
est effectivement un entier, disons

et de montrer qu'alors

est à la fois pair et impair (ce qui contredit l'hypothèse).
1)  est impair :
est impair :On regarde l'équation
\ell=3^p-1)
modulo

. On remarque facilement que pour

pair

et pour n'importe quel

on a

. Pour

pair on a donc
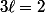
qui n'a pas de solution (multiplier par

des deux côtés pour s'en convaincre).
Donc

est impair. Disons
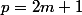
pour la suite.
2)  est pair :
est pair :Pour simplifier on pose
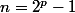
.
L'idée est la suivante : on a

par hypothèses et on va montrer que pour les

de cette forme on a nécessairement

d'ordre pair dans
^\times)
ce qui impliquera que

est pair.
On pose
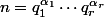
la décomposition de

en facteurs premiers. On va montrer que

n'est pas un carré modulo l'un des
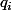
au moins, ce qui est équivalent au fait que

est l'ordre pair modulo
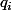
et ce qui implique qu'il est d'ordre pair modulo
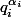
. Il suffira de conclure à l'aide du théorème des restes qui dit en particulier que l'ordre de

dans
^\times)
est le plus petit multiple commun des ordres modulo
^\times)
et est donc pair.
Pour ça on pose
)
le symbole de Legendre de

modulo
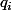
qui vaut

si

est un carré modulo
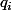
et

sinon. Par la loi de réciprocité quadratique on a
=(-1)^{\frac{q_i-1}{2}}\left(\frac{q_i}{3}\right))
En passant puissance
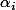
le produit sur

donne
^{\alpha_i}=(-1)^{\sum_i\alpha_i\frac{q_i-1}{2}}\left(\frac{n}{3}\right))
Or on sait que
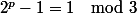
qui est un carré car

est impair.
On veut maintenant montrer que
^{\sum_i\alpha_i\frac{q_i-1}{2}}=-1)
On a,
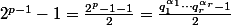
Puisque

est impair tous les
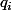
sont impair, disons
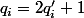
(donc
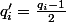
) ce qui donne
^{\alpha_1}\cdots (2q_r'+1)^{\alpha_r}-1}{2})
et en regardant ça modulo

on a
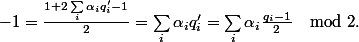
Conclusion :
^{\alpha_i}=-1)
donc au moins un des facteurs vaut
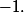
Donc

est d'ordre pair dans
^\times)
donc dans
^\times)
. Donc

est pair.
Donc
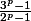
n'est jamais un entier.
Je sais que la démonstration est longue est technique mais je suis persuadé qu'on peut en trouver une plus courte avec des outils plus simples. Je ne sais pas du tout quel est ton niveau, désolé si c'est des outils que tu ne connais pas. Honnêtement, je ne m'attendais pas à devoir déployer un tel arsenal pour cette question. On voit le symbole de Legendre, la réciprocité quadratique, la structure de groupe de
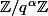
en M1 généralement. N'hésite pas à me demander des détails des affirmations que j'ai laissé sous le tapis (l'ordre d'un élément d'un produit de groupes est le plus petit multiple commun des ordres dans chaque composante, un élément est d'ordre pair dans les inversibles d'un corps fini si, et seulement si, ce n'est pas un carré, l'ordre de l'image d'un élément par la projection
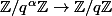
divise l'ordre de son antécédent etc.)
(ne te force pas à essayer de tout déchiffrer par politesse si tu n'y comprends rien, ça m'a fait super plaisir de réfléchir sur cette question).
PS : Dans le premier cas on montre plus généralement que si
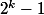
divise
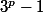
alors

est impair et dans le second cas on montre que si
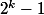
divise
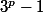
avec

impair alors

pair. Le résultat final est juste une conséquence de ça pour
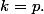
n'est pas un entier, histoire de pouvoir ensuite travailler sur des inégalités strictes.
n'est jamais un entier.
n'est jamais un entier.
est un entier pour
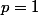
où A et B sont des entiers.
, non ?
