Paradoxe ...

[FLBP]

J'ai trouvé cette petite astuce, je vous en dit pas plus:

soit
Trouvons F(x) en intégrant par partie:







D'où apparait ce 1 ?

[mathelot]

le calcul de primitives se fait modulo une constante d'intégration

[MMu]

Purée, le paradoxe du 21ème siècle ...

[FLBP]

Purée, le paradoxe du 21ème siècle ...

fait gaffe, on est qu'au début ... ahah

[Ben314]

De toute façon, des "paradoxes" consistant à écrire un truc avec des points de suspension (infinis) sans rien expliciter concernant les "restes" de la série, tu peut en trouver autant que tu veut.
Je pense l'avoir dit déjà des tonnes de fois, mais c'est là le "revers de la médaille" du succès des travaux de Cantor concernant "l'infini actuel" : ça donne l'impression à certains qu'on peut "manipuler l'infini" (donc par exemple une somme infinie) comme si c'était un objet "banal" alors que bien évidement, ce n'est absolument pas le cas.
Si Cantor, à son époque, avait autant de détracteur (par exemple Kronecker pour ne citer que le plus célèbre) il faut bien se dire que c'est pas pour rien : apprendre à "maîtriser l'infini", ça ne c'est pas fait en un jour et ce n'est pas parce qu'aujourd'hui tout les matheux le font quotidiennement que ça signifie que le concept de l'infini actuel est un concept "simple à comprendre".

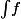
Et bien sûr, il y a aussi l'énorme problème de la notation sans bornes pour désigner UNE primitive de (perso, quand j'enseigne les primitives, je n'utilise jamais cette notation : on s'en passe très facilement sans alourdir considérablement le discours).

[Lostounet]

Salut,

Alors où est l'erreur?

Déjà il y a un truc que j'ai pas compris: pourquoi on remplace le DSE par e^(x)-1 ?
On est pas au voisinage de zéro .. Si ?

Sinon moi ça me gêne pas l'infinité d'intégrations par parties :p
Ça peut se justifier ?

[Ben314]

Sinon moi ça me gêne pas l'infinité d'intégrations par parties :p
Ça peut se justifier ?

Ca pourrait éventuellement si on avait effectivement affaire à une vrai fonction (en montrant que les restes tendent vers 0 bien sûr), mais là, vu que d'écrire ça ne définit rien du tout (*), je vois pas ce que tu peut bien majorer.
Donc si tu veut voir si la série converge ou diverge, ben faudrait commencer par écrire quelque chose qui ait du sens, par exemple . Ensuite, là, oui, tu va pouvoir regarder si la série converge ou pas, mais ça risque bien évidement de dépendre des valeurs de et de .

(*) Et si tu pense que ça défini quelque chose, ben dit moi combien ça vaut F(0) [je rappelle qu'ici, on connaît parfaitement la fonction f)