Paradoxe :interpolation unique et choix multiple de pente

[ArchiCube]

bonjour,

soit une liste de points 2D ou 3D
a)à cette liste,les mathématiques fournissent une seule équation passant par chacun de ces points:c'est l'interpolation de Lagrange y=f(x)
b)Or une fois la courbe d'interpolation tracée,je peux modifier de façon infinie la pente en chacun des ces points
donc une infinité de nouvelles courbes possibles.
exemple:
prenons la liste des points autour d'un cercle de rayon R et répartis selon une même différence d'angle.
La courbe la plus simple passant par tous ces points est le cercle en question
On peut modifier cette interpolation en lui faisant prendre la forme d'une sinusoïde le long de ce cercle passant par cette même liste de points
etc...

Pourtant,malgré l'unicité de la 1ère interpolation deLagrange a) ,j'obtiens une unique dérivée y'=f'(x) contraire au caractère infini de b)
Où est l'erreur causé par ce paradoxe?

merci de votre aide

[ArchiCube]

l'erreur vient du fait qu'il faut commencer à créer une interpolation unique à partir de la liste de vecteurs pentes pour obtenir par intégration à une constante près l'interpolation de la courbe passant par la liste des points.

[GaBuZoMeu]

Tu as l'air d'avoir des idées pas mal confuses.
L'interpolation de Lagrange en n+1 points dans le plan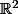 d'abscisses fournit un unique polynôme de degré n dont le graphe passe par ces n+1 points
Si en ces n+1 points tu te donnes en plus des tangentes (non verticales), l'interpolation d'Hermite fournit un unique polynôme de degré 2n+1 dont le graphe passe par les n+1 points et y a pour tangentes les tangentes données.
Si tes n+1 points sont sur un cercle, ni l'interpolation de Lagrange ni celle d'Hermite ne te redonneront le cercle, pour la simple raison qu'aucun arc de cercle n'est le graphe d'un polynôme.