Montrer qu'il existe un seul
Unique
11 messages
- Page 1 sur 1
Unique
Soient  un réel positif et
un réel positif et 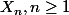 une suite croissante de réels positifs tels que
une suite croissante de réels positifs tels que 
Montrer qu'il existe un seul tel que :
tel que : 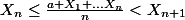
Montrer qu'il existe un seul
Pour l'existence :
Puisque pour tout n, l'inégalité suivante qui est strictement positif.
qui est strictement positif.
Je réfléchis encore à une manière de concilier le rang n que je viens de trouver avec un rang n1 correspondant à l'inégalité de gauche... En tout cas il faut vraisemblablement que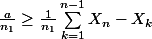)
Sans certitudes toutefois... :/
PS : Je retire ce que j'ai dit pour l'inégalité de droite. Il existe un bogue... Rien ne garantit que lorsque n devient grand, la quantité a/n décroit assez vite pour se trouver en-dessous de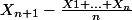
Puisque pour tout n, l'inégalité suivante
Je réfléchis encore à une manière de concilier le rang n que je viens de trouver avec un rang n1 correspondant à l'inégalité de gauche... En tout cas il faut vraisemblablement que
Sans certitudes toutefois... :/
PS : Je retire ce que j'ai dit pour l'inégalité de droite. Il existe un bogue... Rien ne garantit que lorsque n devient grand, la quantité a/n décroit assez vite pour se trouver en-dessous de
On a
x1 x2-x1
x3 2x3-(x1+x2)
et plus généralement
x(n+1) n*x(n+1)-(x1+x2+..xn)=En
Mais est ce tjs vrai, avec a fixé, si n ---> oo ?
En=(x(n+1)-xn)+(x(n+1)-x(n-1))+...(x(n+1)-x1)
En supposant une progession minimale de la suite des x, soit x(n+1)=xn+ 1/n² on a:
En=1/n²+(1/n² + 1/(n-1)²)+(1/n² + 1/(n-1)² + 1/(n-2)²)+.....=
n/n²+(n-1)/(n-1)² + (n-2)/(n-2)²+....=
1/n+1/(n-1)+1/(n-2)+....
Somme minimale qui est divergente.
Il n'existe pas de a suffisamment grand pour être tjs au dessus de En.
Il arrivera donc que pour une valeur de n on aura:
(a+x1+..xn)/n1
Par récurrence:
a+x1+..xn < n*x(n+1)
a+x1+..x(n+1) < (n+1)*x(n+1) < (n+1)* x(n+2).
Donc (a+x1+..x(n+1)/(n+1) < x(n+2)
x1 x2-x1
x3 2x3-(x1+x2)
et plus généralement
x(n+1) n*x(n+1)-(x1+x2+..xn)=En
Mais est ce tjs vrai, avec a fixé, si n ---> oo ?
En=(x(n+1)-xn)+(x(n+1)-x(n-1))+...(x(n+1)-x1)
En supposant une progession minimale de la suite des x, soit x(n+1)=xn+ 1/n² on a:
En=1/n²+(1/n² + 1/(n-1)²)+(1/n² + 1/(n-1)² + 1/(n-2)²)+.....=
n/n²+(n-1)/(n-1)² + (n-2)/(n-2)²+....=
1/n+1/(n-1)+1/(n-2)+....
Somme minimale qui est divergente.
Il n'existe pas de a suffisamment grand pour être tjs au dessus de En.
Il arrivera donc que pour une valeur de n on aura:
(a+x1+..xn)/n1
Par récurrence:
a+x1+..xn < n*x(n+1)
a+x1+..x(n+1) < (n+1)*x(n+1) < (n+1)* x(n+2).
Donc (a+x1+..x(n+1)/(n+1) < x(n+2)
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
