Salut,
J'ai l'impression que ça marche dans tout les cas le truc d'aviateur modulo d'ajouter quelques précisions :
1) Au départ, ça ne sert à rien de supposer le corps de caractéristique 0 : pour faire sa construction, il suffit de supposer qu'il est infini et de prendre les polynômes
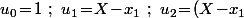(X\!-\!x_2)\,,\cdots)
où
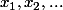
sont des éléments distincts de

.
Et on peut faire remarque en amont que de toute façon, si le corps

est fini, le résultat est trivialement vrai vu que toute fonction de

dans

et plus généralement de
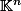
dans

est polynomiale.
2) Et à la fin, la preuve fonctionne (modulo de préciser que l'on prend l'ensemble des racines des polynômes
non nuls parmi les a_k, mais je chipotte...) pour n'importe quel corps infini non dénombrable.
Bref, il reste uniquement le cas des corps infini dénombrables, sauf que j'ai l'impression que dans ce cas là, ça marche pas : si
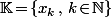
et qu'on pose
\!=\!\prod_{k=0}^n(X\!-\!x_k))
puis
\!=\!\sum_{n=0}^{\infty}P_n(x)P_n(y))
alors, pour un
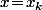
fixé de

on a
\!=\!\sum_{n=0}^{k-1}P_n(x_k)P_n(y))
vu que
\!=\!0)
pour
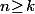
donc c'est bien un polynôme en

. Par contre,

n'est pas un polynôme vu que les degré des polynômes
)
peuvent être arbitrairement grand (et comme le corps est infini, il n'y a qu'une seule représentation sous forme de polynôme)