Défi 38
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 15 Fév 2007, 18:09
par Imod » 15 Fév 2007, 18:09
Bonjour à tous .
Un petit défi qui nest pas sans rappeler les sangakus japonais . Un triangle

et un entier
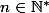
donnés , on considère :

,

,

, ... ,

points de
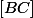
, de façon à ce que les diamètres

des cercles inscrits dans
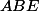
,

,

, ... , soient égaux . Dans

, on note

la hauteur issue de

et

le diamètre du cercle inscrit . Exprimer

à l'aide de

,

, et

.
Une illustration avec
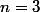
:

Le résultat est très simple et la solution courte , mais il faut avoir la bonne idée .
Bon courage !
Imod
-
mathelot
 par mathelot » 15 Fév 2007, 23:09
par mathelot » 15 Fév 2007, 23:09
hello,
tous les petits triangles ont la même hauteur. On calcule leur aire
Et puis, il doit y avoir une relation entre le rayon du cercle inscrit et l'aire
ie, S=pr avec p le demi-périmètre ? :id:
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 15 Fév 2007, 23:47
par Imod » 15 Fév 2007, 23:47
mathelot a écrit:hello,
tous les petits triangles ont la même hauteur. On calcule leur aire
Et puis, il doit y avoir une relation entre le rayon du cercle inscrit et l'aire
ie, S=pr avec p le demi-périmètre ? :id:
Tu risques de peiner avec les demi-périmètres : la solution est simple mais pas l'idée qui l'induit .
Imod
PS : Je suis né à Enghien-les-bains et j'ai passé mes cinq premières années à Franconville , mais tout celà c'est la préhistoire :we:
-
maf
- Membre Rationnel
- Messages: 911
- Enregistré le: 08 Jan 2007, 17:57
-
 par maf » 16 Fév 2007, 12:31
par maf » 16 Fév 2007, 12:31
J'ai essayé de jouer avec le fait que les angles entres les centres des cercles et les points de tangences se rapportent 2 à 2 entres les petits cercles ... et que les 2 petits cercles d'extrémité ont les mêmes angles que le grand ...
Mais ... j'aboutis à pas grand chose :briques:
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Fév 2007, 17:33
par Imod » 16 Fév 2007, 17:33
Une petite aide pour démarrer ce défi .
Dans le grand triangle

, on peut exprimer

à l'aide de

et

(en utilisant les différentes formules d'aire ) .
La suite est magnifique !
Imod
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 18 Fév 2007, 00:41
par Imod » 18 Fév 2007, 00:41
Je donne la réponse à l'indice fourni , pour ceux qui veulent essayer de le justifier et surtout pour ceux qui verront ce qu'on peut en tirer :
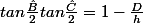
Imod
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 21 Fév 2007, 19:13
par Imod » 21 Fév 2007, 19:13
Dernier indice :
Quelles égalités donne la dernière relation si on l'applique à chacun des triangles contenant un petit cercle ? Qu'obtient-on en multipliant ces égalités entre-elles ?
Imod
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 22 Fév 2007, 17:58
par Imod » 22 Fév 2007, 17:58
Une solution .
On note :
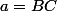
,
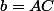
,
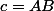
,
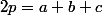
,

et

le rayon et le diamètre du cercle inscrit dans

et

l'aire de

.

On a :
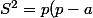(p-b)(p-c))
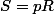
donc
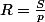
.
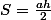
donc
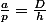
Alors :
}.\frac{S}{p(p-c)}=\frac{p(p-a)(p-b)(p-c)}{p^2(p-b)(p-c)}=\frac{p-a}{p}=1-\frac{a}{p}=1-\frac{D}{h}})
.
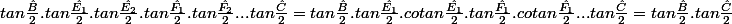
.
En effet , les angles

et

sont complémentaires donc
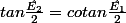
. Et comme
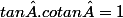
, on a le résultat .
Appliquons maintenant la formule précédente à

et chacun des petits triangles
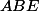
,

,

, ... :
^n=1-\frac{D}{h})
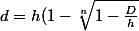)
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 347 invités


