Inégalité et factorisation

par **most** » 03 Oct 2010, 23:10

bonjour, est ce que quelqu'un peut montrer que :
1) pourtout x,y,z>4 : si xy < z alors x+y 2) factoriser x^8 +x+1
3) factoriser x^10 +x^5 +1
merci pour tous

par **Olympus** » 04 Oct 2010, 00:14

Salut !

Rapidement puisque c'est tard et que je dois y aller :

1) On suppose que

Donc

et

2)

( cette méthode n'est sûrement pas la plus jolie, si quelqu'un aurait une meilleure méthode je serais bien intéressé )

On cherchera deux polynômes à coefficients entiers de degrés 2 et 6, 3 et 5 ou 4 et 4 .

On commencera par le 2 et 6, et si par miracle on arrive à des polynômes candidats qui marchent, alors pas la peine d'essayer les autres cas .

Où

Et

.

Vu que

, on a

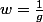
Donc

.

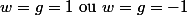
Donc

ou

.

Traitons le premier cas .

On a

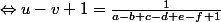
Donc

OU

.

Traitons le premier cas, donc

.

.

Le coefficient de

dans

est

, alors soit

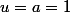
, soit

.

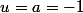
Donc

ou

.

On va les tester en divisant P par Q, on commencera par le premier cas, on aura :

Donc notre Q convient, et plus la peine de tester les autres cas car on a trouvé ce qu'on recherchait .

Pour la 3), pas le temps, mais je crois que ça se fait de la même manière .

PS : je séchais sur la 2 y a 2 ans :ptdr:

par **mathelot** » 04 Oct 2010, 05:58

Bonjour,

pour la (3) , x racine alors

vaut

ou

une possibilité est donc de calculer avec

mais

en effet les facteurs trinômes pour des racines de l'unité sont de la forme

par **mathelot** » 04 Oct 2010, 06:18

la (2) admet

et

pour racines évidentes
ça se factorise par

par **most** » 04 Oct 2010, 07:12

bien joué, merci pour le temps consacré .
pour

est solution de

soit

0 puis
changement de variable

par **mathelot** » 04 Oct 2010, 08:02

most a écrit:bien joué, merci pour le temps consacré .
pourest solution de soit 0 puis
changement de variable

oui, tout à fait

par **Olympus** » 04 Oct 2010, 12:44

Effectivement, avec les complexes ça se torche très facilement, mais j'avais cet exercice lors des olympiades de 2ndes, donc je ne pense pas que la méthode par les complexes était celle qui était attendu .

par **mathelot** » 04 Oct 2010, 16:29

Olympus a écrit:cette méthode n'est sûrement pas la plus jolie, si quelqu'un aurait une meilleure méthode je serais bien intéressé

je ne pense pas que la méthode par les complexes était celle qui était attendue

Bah après, il reste la méthode de Newton :we:

par **Olympus** » 04 Oct 2010, 18:32

Je ne nie pas que la tienne est plus jolie que la mienne ^^

Mais je disais juste que si on me l'avait posé aux olympiades de 2nde, alors il doit bien y avoir une méthode courte de niveau 2nde . J'ai parcouru le livre "Polynomials" de E.J. Barbeau et j'ai juste trouvé la méthode que j'ai énoncé plus haut ( exploiter le fait que les coefficients des deux polynômes sont entiers et faire un peu d'arithmétique ) .

par **Lostounet** » 25 Oct 2010, 16:03

Olympus a écrit:Mais je disais juste que si on me l'avait posé aux olympiades de 2nde.

Il y a des olympiades de 2nde? :bad:

par **Olympus** » 25 Oct 2010, 19:46

Lostounet a écrit:Il y a des olympiades de 2nde? :bad:

Ouép, enfin, chez nous au moins ^^

Inégalité et factorisation

inégalité et factorisation

Qui est en ligne