Si l'on demande a quelqu'un de choisir un chiffres entre 0 et 9, si l'on ne s'occupe que des entier naturels la probabilité que l'on trouve son nombre et de 1/10 soit 0,1. Maintenant même question mais pour un nombre choisis entre 0 et ∞ dans les entiers naturels ?
Si l'on voit les chose sous frome de liste choisir un chiffres entre 0 et 9 revient a prendre un élément aléatoirement d'une liste a 10 éléments contenant (0,1,2,...,8,9). La logique voudrait donc que pour un nombre choisis entre 0 et ∞, cela reviendrait a prendre un élément aléatoirement d'une liste a ∞ éléments contenant (0,1,2,...,∞). Soit une probabilité de 1/∞, dans les calculs de limites cela vaut 0. Mais cela pose deux paradoxe...
Le premier c'est que l'on ne peut pas choisir l'infini comme réponse si l'on demande a quelqu'un de choisir un chiffres entre 0 et ∞ car il n'est pas caractérisable.
Et le deuxième c'est qu'il y a toujours une chance même infime que je trouve le chiffre choisit.
On note P(n) la probabilité de trouver le nombre choisi, en sachant qu'il est compris entre 0 et n et que c'est un entier naturel.
Votre question est de trouver P(∞) ?
Et pour les plus téméraire vous pouvez également prouver que P(∞)>P(∞+1)
Bonne chance !!
Probabilité équivalent a l'infini
10 messages
- Page 1 sur 1
Re: Probabilité équivalent a l'infini
Bonjour,
Désolé aquada, mais ce que tu racontes n'a pas de sens mathématique. Il n'y a pas de mesure de probabilité uniforme sur l'ensemble des entiers naturels ; qu'on y ajoute ou pas ne change d'ailleurs rien à l'affaire.
ne change d'ailleurs rien à l'affaire.
Désolé aquada, mais ce que tu racontes n'a pas de sens mathématique. Il n'y a pas de mesure de probabilité uniforme sur l'ensemble des entiers naturels ; qu'on y ajoute ou pas
Re: Probabilité équivalent a l'infini
De plus, tu verras peut-être plus tard que la probabilité zéro ne signifie pas que l'événement est impossible.
Chaîne Youtube - Au Coeur des Sciences : https://www.youtube.com/@AuCoeurDesSciences
Re: Probabilité équivalent a l'infini
Pour résumer, Spalding raconte n'importe quoi, comme d'hbitude.
L'argument diagonal de Cantor démontre bien que pour toute application de
de  dans
dans 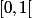 , il existe au moins un élément de
, il existe au moins un élément de 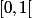 (construit explicitement à partir de
(construit explicitement à partir de  ) qui n'est pas dans l'image de
) qui n'est pas dans l'image de  . Dans la théorie des ensembles initiée par Cantor, cela veut dire très précisément que le cardinal de
. Dans la théorie des ensembles initiée par Cantor, cela veut dire très précisément que le cardinal de  est strictement plus petit que celui de
est strictement plus petit que celui de 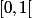 , et donc aussi de celui de
, et donc aussi de celui de  .
.
L'argument diagonal de Cantor démontre bien que pour toute application
Re: Probabilité équivalent a l'infini
Bonjour, on va la faire courte, je n'ai pas lu le message de Spalding et je déconseille à tous les lecteurs de le faire car il troll en provoquant les intervenants compétents.
Heureusement aquada ne reviendra vraisemblablement pas sur ce sujet donc c'est sans grande importance.
Je cite le message d'un des seuls modérateurs encore présent https://www.maths-forum.com/cafe-mathematique/reponses-sur-nombre-infini-t252987.html
Heureusement aquada ne reviendra vraisemblablement pas sur ce sujet donc c'est sans grande importance.
Je cite le message d'un des seuls modérateurs encore présent https://www.maths-forum.com/cafe-mathematique/reponses-sur-nombre-infini-t252987.html
@spalding
tu n'es pas non plus le(la) bienvenue sur maths-forum.
raisons:
pas de changement de comportement
des incessants pavés
que des piques plutot que de se concentrer sur le contenu
le word inchangé avec un potentiel nuisible pour les étudiants
enfin, on sait très bien que cette discussion n'avancera ordinalement que dans son cardinal de message ...
Je ferme et t'invite @spalding à ne pas revenir ici
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
Re: Probabilité équivalent a l'infini
Belle escroquerie de Spalding :
C'est bien sûr totalement faux : Spalding prétend qu'il y a "bien évidemment" une injection de dans
dans  , qui associe à un touriste réel son n° de chambre. Comme l'inclusion fournit une injection de
, qui associe à un touriste réel son n° de chambre. Comme l'inclusion fournit une injection de  dans
dans  , le théorème de Cantor Bernstein entraînerait alors qu'il y a une bijection de
, le théorème de Cantor Bernstein entraînerait alors qu'il y a une bijection de  sur
sur  , et l'argument diagonal de Cantor DÉMONTRE que c'est imposible.
, et l'argument diagonal de Cantor DÉMONTRE que c'est imposible.
Comment fait Spalding pour trouver valable une théorie dont il ne comprend pas les théorèmes les plus élémentaires ?
Mais il est évident que tous les touristes (nombres réels) pourront être logés dans les chambres numérotées selon l'ordre des nombres naturels (entiers), même s'il faudra un temps infini. Par conséquent, on voit bien que le nombre infini des nombres réels n'est pas supérieur au nombre infini des nombres naturels !
C'est bien sûr totalement faux : Spalding prétend qu'il y a "bien évidemment" une injection de
Sans être spécialiste, la théorie des ensembles de Cantor paraît tout à fait valable.
Comment fait Spalding pour trouver valable une théorie dont il ne comprend pas les théorèmes les plus élémentaires ?
Re: Probabilité équivalent a l'infini
GaBuZoMeu est manifestement moins bien placé que moi pour en parler, car il n'a pas lu un seul livre sur ses théories, même de vulgarisation !





Aucun mathématicien à l'heure actuelle ne met en doute l'argument diagonal de Cantor. Les objections de Kronecker étaient d'ordre idéologique : refus de travailler avec l'infini actuel, autrement dit de considérer l'ensemble des entiers naturels ou l'ensemble des nombres réels (sans autre structure que celle d'ensemble) comme un objet mathématique sur lequel on peut raisonner. Mais c'est justement l'essence de la théorie des ensembles, que Spalding trouve "valable" sans en connaître le b-a-ba et en n'ayant pas peur de se contredire avec son refus de la théorie des cardinaux qui découle de la théorie des ensembles.
Spalding prétend sans aucun argument autre qu'un baratin fumeux que deux ensembles infinis quelconques peuvent être mis en bijection "au hasard". C'est du n'importe quoi qui n'a rien à voir avec des mathématiques.
J'ai aussi donné un exemple très concret, auquel GaBuZo Meu n'a pas du tout répondu. Je comprends que cela le gêne !
Aucun exemple concret dans le baratin de Spalding, juste l'affirmation que'"il est évident que tous les touristes (nombres réels) pourront être logés dans les chambres numérotées selon l'ordre des nombres naturels (entiers)", ce qui est évidemment faux comme je l'ai montré.
Spalding enfile tant de contrevérités qu'il m'est difficile de penser qu'il croit lui-même à ce qu'il raconte. Ou alors, c'est grave pour lui.
Re: Probabilité équivalent a l'infini
Spalding, une petite question à laquelle tu peux répondre par oui ou non : une "bijection au hasard" d'un ensemble  sur un ensemble
sur un ensemble  est-elle une application bijective ?
est-elle une application bijective ?
(Je suppose que tu sais ce qu'est une application bijective entre deux ensembles, sinon je t'en donne la définition).
(Je suppose que tu sais ce qu'est une application bijective entre deux ensembles, sinon je t'en donne la définition).
Re: Probabilité équivalent a l'infini
A mon avis tu perds ton temps GaBuZoMeu a vouloir donner du sens aux propos de Spalding, voir ses fameuses bijections au hasard https://les-mathematiques.net/vanilla/index.php?p=/discussion/2257850/les-nombres-infinis-selon-cantor
Mais je sais que tu aimes les challenges et puis certains diraient que tu es de l'école "c'est plus beau quand c'est inutile" donc je ne voudrais pas te gâcher ton plaisir d'autant plus qu'il y a un certain panache à répondre mathématiquement à tous les hurluberlus des internets.
Mais je sais que tu aimes les challenges et puis certains diraient que tu es de l'école "c'est plus beau quand c'est inutile" donc je ne voudrais pas te gâcher ton plaisir d'autant plus qu'il y a un certain panache à répondre mathématiquement à tous les hurluberlus des internets.
Merci aux enseignants (ou autres) qui partagent leurs connaissances reconnues par le consensus scientifique, permettent à des individus de se construire et à la société d'évoluer.
Re: Probabilité équivalent a l'infini
Rassure-toi, Kekia, je ne cherche pas à donner du sens au baratin de Spalding, je sais bien qu'il n'y en a pas.
Rien ne nouveau dans sa nouvelle livraison, à part des bêtises supplémentaires dans l'analyse de l'argument diagonal de Cantor. Et toujours la même affirmation aberrante sur les touristes (réels) et les chambres (entiers naturels) : "Mais tous sans exception auront une chambre ! ", autrement dit il y a une application injective de l'ensemble des réels dans l'ensemble des entiers naturels ; c'est une évidence, selon Spalding : pas besoin de démonstration. Le théorème de Cantor-Bernstein et l'argument diagonal de Cantor démontrent que c'est faux, mais peu importe pour Spalding !
La longueur de la prose ne comble pas le vide scientifique.
Et bien sûr, aucune réponse à ma question précise : est-ce qu'une "bijection au hasard" entre l'ensemble X et l'ensemble Y est une application bijective de X sur Y ?
Je vais plutôt essayer de donner quelques informations qui pourraient être utiles pour qui n'est pas très familier avec cette notion de cardinal.
Le cardinal d'un ensemble X est inférieur ou égal au cardinal de l'ensemble Y quand il existe une application injective de X dans Y.
Le théorème de Cantor-Bernstein montre que s'il y a une application injective de X dans Y et une application injective de Y dans X, alors il y a une application bijective de X sur Y. Dans ce cas le cardinal de X est égal au cardinal de Y (X et Y sont équipotents).
Il y a une application injective de dans
dans  : l'inclusion, tout simplement. Il n'y a aucune application injective de
: l'inclusion, tout simplement. Il n'y a aucune application injective de  dans
dans  : s'il y en avait, le théorème de Cantor-Bernstein montrerait qu'il y a une bijection de
: s'il y en avait, le théorème de Cantor-Bernstein montrerait qu'il y a une bijection de  sur
sur  , ce qui est exclu par l'argument diagonal de Cantor. Le cardinal de
, ce qui est exclu par l'argument diagonal de Cantor. Le cardinal de  , est donc strictement plus grand que celui de
, est donc strictement plus grand que celui de  .
.
Revenons sur l'argument diagonal de Cantor. Une variante simple montre qu'il n'y a pas d'application surjective de dans
dans 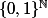 , l'ensemble des suites de 0 et de 1. En effet, si
, l'ensemble des suites de 0 et de 1. En effet, si  est une application de
est une application de  dans
dans 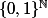 , alors la suite
, alors la suite 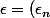) définie par
définie par 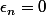 si
si _n=1) et
et 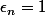 si
si _n=0) n'est pas dans l'image de
n'est pas dans l'image de  . Si l'on a écrit
. Si l'on a écrit  sous forme d'un tableau dont les lignes sont les suites
sous forme d'un tableau dont les lignes sont les suites ) ,
, ) etc. ce qu'on a fait est changer les 0 en 1 et vice-versa dans la diagonale du tableau pour fabriquer
etc. ce qu'on a fait est changer les 0 en 1 et vice-versa dans la diagonale du tableau pour fabriquer  .
.
L'ensemble) des parties de
des parties de  peut s'identifier à
peut s'identifier à 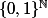 en associant à chaque partie
en associant à chaque partie  de
de  sa fonction caractéristique
sa fonction caractéristique 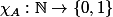 définie par
définie par =1) si
si 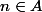 et
et  sinon. Autrement dit,
sinon. Autrement dit, 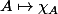 est une bijection de
est une bijection de ) sur
sur 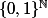 . L'argument diagonal de Cantor que l'on vient d'expliquer se généralise alors de
. L'argument diagonal de Cantor que l'on vient d'expliquer se généralise alors de  à n'importe quel ensemble
à n'importe quel ensemble  pour montrer qu'il n'existe pas de surjection de
pour montrer qu'il n'existe pas de surjection de  sur
sur ) , l'ensemble des parties de
, l'ensemble des parties de  . Voici comment :
. Voici comment :
Soit une application de
une application de  dans
dans ) . Définissons la partie
. Définissons la partie  de
de  comme l'ensemble des éléments
comme l'ensemble des éléments  de
de  tels que
tels que ) ; dans le cas
; dans le cas 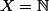 , la fonction caractéristique de
, la fonction caractéristique de  est précisément le
est précisément le 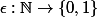 construit plus haut. Alors
construit plus haut. Alors  n'est pas dans l'image de
n'est pas dans l'image de  . En effet, supposons que
. En effet, supposons que ) pour un élément
pour un élément  de
de  . Si
. Si =A) , alors
, alors ) par définition de
par définition de  : absurde. Si
: absurde. Si ) , alors, par définition de
, alors, par définition de  ,
, 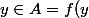) : absurde. Ceci montre qu'aucune application de
: absurde. Ceci montre qu'aucune application de  dans
dans ) n'est surjective.
n'est surjective.
On a une application injective de dans
dans ) : celle qui envoie chaque élément
: celle qui envoie chaque élément  de
de  sur le singleton
sur le singleton ) . Il n'y a pas d'application injective de
. Il n'y a pas d'application injective de ) dans
dans  d'après le théorème de Cantor-Bernstein et le fait qu'il n'y a pas de surjection de
d'après le théorème de Cantor-Bernstein et le fait qu'il n'y a pas de surjection de  sur
sur ) . Le cardinal de
. Le cardinal de  est donc strictement plus petit que celui de
est donc strictement plus petit que celui de ) .
.
Supposons infini. On se retrouve avec pléthore de cardinaux infinis différents : ceux de
infini. On se retrouve avec pléthore de cardinaux infinis différents : ceux de ,\mathcal P(\mathcal P(X)),\ldots) . C'est un résultat élémentaire de théorie des ensembles.
. C'est un résultat élémentaire de théorie des ensembles.
Rien ne nouveau dans sa nouvelle livraison, à part des bêtises supplémentaires dans l'analyse de l'argument diagonal de Cantor. Et toujours la même affirmation aberrante sur les touristes (réels) et les chambres (entiers naturels) : "Mais tous sans exception auront une chambre ! ", autrement dit il y a une application injective de l'ensemble des réels dans l'ensemble des entiers naturels ; c'est une évidence, selon Spalding : pas besoin de démonstration. Le théorème de Cantor-Bernstein et l'argument diagonal de Cantor démontrent que c'est faux, mais peu importe pour Spalding !
La longueur de la prose ne comble pas le vide scientifique.
Et bien sûr, aucune réponse à ma question précise : est-ce qu'une "bijection au hasard" entre l'ensemble X et l'ensemble Y est une application bijective de X sur Y ?
Je vais plutôt essayer de donner quelques informations qui pourraient être utiles pour qui n'est pas très familier avec cette notion de cardinal.
Le cardinal d'un ensemble X est inférieur ou égal au cardinal de l'ensemble Y quand il existe une application injective de X dans Y.
Le théorème de Cantor-Bernstein montre que s'il y a une application injective de X dans Y et une application injective de Y dans X, alors il y a une application bijective de X sur Y. Dans ce cas le cardinal de X est égal au cardinal de Y (X et Y sont équipotents).
Il y a une application injective de
Revenons sur l'argument diagonal de Cantor. Une variante simple montre qu'il n'y a pas d'application surjective de
L'ensemble
Soit
On a une application injective de
Supposons
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
