Réponses sur le nombre infini

[Spalding]

Le modérateur a verrouillé mon sujet sur "L’infini est-il un nombre ?", pour lequel je n’avais mis que 2 messages (page 1). Ils ont attiré pas moins de 60 réponses (excusez du peu), qualifiées par le modérateur de "déchetterie à ciel ouvert" : des règlements de compte personnels ! Le même phénomène s’était produit sur un autre forum de maths, aussi sur ce forum avec mon sujet sur "Les méthodes pour arrondir un nombre". Personne ne s’est donné la peine de lire mon fichier (7 pages) pour un projet d’article Wikipédia : https://www.aht.li/3674142/ARRONDIR.pdf

Je pensais continuer avec les idées du mathématicien Cantor sur le nombre infini, plutôt les nombres infinis pour lui avec certains supérieurs à d’autres : une conception critiquée par d’autres mathématiciens (Kronecker notamment). De mon point de vue, il n’existe aussi qu’un seul nombre infini (cardinal). Mais comme beaucoup de participants à ce forum ne savent manifestement pas se comporter dans une discussion, je laisse tomber ! Je vais juste répondre aux quelques critiques précises (de fond) dans mon sujet verrouillé sur "L’infini est-il un nombre ?".


1) Lycéen-95 me dit que je n’ai pas bien défini les nombres cardinal et ordinal. Je pense avoir été parfaitement clair dans mon premier message du sujet "L’infini est-il un nombre ?". Un nombre cardinal indique une quantité, un nombre ordinal une position ! Si une pièce carrée a 3,45 mètres de côté, c’est une quantité cardinale. Mais si quelqu’un est à 3,45 mètres (distance) d’une autre personne, c’est une position ordinale ! Si la taille d’un homme est 1,86 mètre, c’est une quantité cardinale. Mais si l’on dit que le crâne de cet homme est à 1,86 mètre (distance) du sol, c’est une position ordinale ! S’il y a 20 cacahuètes sur un plateau d’apéritif, c’est un nombre cardinal (quantité). Mais si l’on en est à sa 20e cacahuète, c’est un nombre ordinal (position) !


2) Lycéen-95 commet par ailleurs une grave erreur en confondant les nombres cardinaux avec les nombres nul et positifs ! Le nombre nul peut indiquer une quantité (cardinale) ou une position (ordinale) selon le cas. Par contre, les nombres négatifs et positifs ont toujours une valeur ordinale, permettant de situer un nombre sur une double échelle par rapport à 0. La température d’une pièce peut être par exemple à –5 ou à +10 degrés, c’est-à-dire respectivement à une distance de 5 et de 10 degrés par rapport à 0. Comme le signe + est souvent omis devant un nombre positif, on a tendance à confondre les nombres cardinaux avec les nombres positifs. Mais cela n’a aucun rapport !

Avec une seule échelle, il est bien sûr inutile d’indiquer – ou + devant un nombre ordinal, par exemple pour la page 250 (nombre ordinal) d’un livre de 250 pages (nombre cardinal).


3) Dans le sujet annexe "Réponse à GaBuZoMeu" (aussi verrouillé), Lycéen-95 affirme qu’un nombre cardinal ne peut être qu’un nombre entier. Nouvelle erreur grave ! Tout dépend du contexte. Dans une classe, on ne peut pas en effet avoir 10,64 élèves. Par contre, on peut très bien avoir une pièce de 10,64 mètres (1.064 centimètres) de long. C’est manifestement une quantité cardinale, pas une position ordinale ! Idem pour les 331,449.281 millions d'Américains au recensement de 2020.

Le nombre Pi (mentionné par Lycéen-95) peut être cardinal ou ordinal selon le contexte. Par exemple, si une pièce a 3,141.592… (Pi) mètres de côté, c’est un nombre cardinal (quantité). Mais si un navire se trouve à 3,141.592… (Pi) degrés de latitude nord, c’est un nombre ordinal (position) !


Je ne continuerai pas ce sujet sur l’infini, vu l’ambiance délétère sur ce forum. Dommage car je pensais qu’on aurait pu avoir une discussion intéressante avec les conceptions de Cantor en la matière (lu un livre là-dessus). Tant pis !

[beagle]

Salut Spalding,

"Je pensais continuer avec les idées du mathématicien Cantor sur le nombre infini, plutôt les nombres infinis pour lui avec certains supérieurs à d’autres : une conception critiquée par d’autres mathématiciens (Kronecker notamment). De mon point de vue, il n’existe aussi qu’un seul nombre infini (cardinal). "

tu aurais du commencer par cela,
parce que là c'est du haut niveau,
puisque tu rejettes l'idée cardinal d'un infini est la mise en bijection...patati...

Donc comme pour la notion de nombre que tu ne définis pas lorsque infini,
quelle notion de cardinal tu utilises si tu rejettes les notions classiques...

[fatal_error]

Bonjour Spalding,

Pour information si tu manques de retour, ton document ne m'intéresse pas vraiment car il est trop verbeux. Aussi, quand je lis des documents c'est pas par hasard, c'est parce que je cherche une information.

Néanmoins quelques problèmes:

- tu l'as rédigé comme un cours et c'est gênant. Cela pourrait perturber les élèves et si tu t'en soucies tu devrais fortement préciser en entête qu'il ne s'agit aucunement d'un cours mais d'un essai amateur. C'est aussi un moyen de faire preuve d'humilité face à la communauté (dont certains sont profs) dont tu demandes une relecture (demande-tu vraiment une relecture?)
- c'est, désolé, confusant, verbeux, et une perte d'énergie mentale (qui voudrait lire 8pages? d'un contenu dont on ne connait pas la problèmatique adressée?)

Côté modération, je n'hésiterai pas s'il le faut à également fermer cette discussion voire bannir si les interventions généraient trop de pollution

PS: tu devrais vraiment faire preuve de modestie. Lycéen95 est peut-être l'un des rares qui ait pris le temps de te répondre.
Si tu continues dans cette lancée, tu te doutes bien de la suite

[Spalding]

@ Beagle -- Dans ce sujet "L'infini est-il un nombre ?", j'ai commencé par exposer ma conception de l'infini comme un nombre cardinal (non ordinal) pouvant donner lieu à des opérations arithmétiques (exposées en détail). J'allais ensuite passer à Cantor pour montrer en quoi sa conception de l'infini est identique et en quoi elle diffère (d'après le livre lu à ce sujet), pourquoi aussi elle est contestée par des mathématiciens. Je l'ai d'ailleurs annoncé à la fin de mon deuxième message. Chaque chose en son temps... Sur ce, on a eu une soixantaine de messages entre les forumeurs pour vider leurs querelles personnelles et le modérateur a dû fermer ce sujet.

@ Modérateur -- Désolé, mais je ne vois pas très bien en quoi mon étude sur "Les méthodes pour arrondir un nombre" est confuse. Elle comporte quatre parties très logiques : généralités, arrondissement sans considérer la proximité des nombres, arrondissement d'un nombre à sa valeur la plus proche, opérations arithmétiques avec les nombres arrondis. Chacune de ces parties comporte des sous-parties. Difficile de faire plus structuré ! On n'a de toute façon pas fait la moindre critique de cette étude ! Je suppose donc que personne ne l'a lue (bien qu'elle n'ait que 7 pages) ou que tout le monde l'a trouvée parfaite ! Dans les deux cas, pourquoi ne me l'a-t-on pas dit au lieu de se lancer dans des querelles personnelles sans aucun rapport ?

@ Lycéen-95 m'a fait des critiques pour mes deux messages de "L'infini est-il un nombre ?". C'est son droit. J'ai moi aussi le droit de répondre à ses critiques. Si je n'ai pas forcément la science infuse, Lycéen-95 non plus !

[lyceen95]

Sur Cantor/Kronecker, je ne vais pas m'aventurer sur ce sujet. Il faut avoir un certain niveau, et je suis conscient de ne pas être compétent. Vas-y Spalding, fais-toi plaisir.
No limit !

[Kekia]

Bonjour,
Pour ceux qui veulent lire des choses sérieuses, il y a déjà eu des personnes qui ont répondu sérieusement à Spalding sur ce sujet ailleurs https://les-mathematiques.net/vanilla/index.php?p=/discussion/2257850/les-nombres-infinis-selon-cantor
Ici, à part GaBuZoMeu, je ne vois pas trop qui aurait le niveau et l'envie pour s'y coller et encore je ne sais pas si il a toujours envie.

[GaBuZoMeu]

Personne ne s’est donné la peine de lire mon fichier (7 pages) pour un projet d’article Wikipédia : https://www.aht.li/3674142/ARRONDIR.pdf

Mensonge caractérisé !
D'ailleurs j'ai répondu très précisément à ta question (assez triviale il suffisait de comprendre ce qu'est la moyenne géométrique) sur "l'arrondi proportionnel" dans le dernier message de ce fil
https://www.maths-forum.com/post1501031.html#p1501031
Tu es resté muet après cette réponse, et maintenant tu te réveilles pour venir une nouvelle fois polluer.

PS. Vu que Spalding a déjà du mal à maîtriser la moyenne géométrique, je me vois mal lui expliquer les ordinaux de Cantor. Juste une petite blague pour nous changer d'omicron. En notant comme d'habitude le premier ordinal infini, .

[Spalding]

Eh ben, tu en as mis du temps pour répondre à ma question ! Tu t'es fait tellement prier que j'ai complètement abandonné ce sujet sans lire ton message in extremis, surtout après toutes les attaques personnelles dont j'ai fait l'objet ! Cela m'avait complètement écœuré ! Quant à cette étude sur l'arrondissement des nombres, je ne prétends pas du tout qu'elle ait un grand intérêt théorique. Elle a surtout une valeur pratique, est en tout cas nettement supérieure à l'article Wikipédia là-dessus. Son auteur ne signale même pas la possibilité d'arrondir des nombres entiers, n'envisage surtout jamais l'arrondissement proportionnel des nombres équidistants, ne s'occupe pas non plus des opérations arithmétiques entre les nombres arrondis. Vous pouvez vous y reporter...

S'agissant de Cantor, je n'ignore aucunement ses ordinaux, vu le livre lu sur ses conceptions. Mais il s'agit alors de sa théorie des ensembles. C'est tout autre chose ! Ce que j'allais précisément envisager, c'est sa conception selon laquelle certains nombres infinis ont une valeur cardinale supérieure à d'autres : une conception très contestée par de nombreux mathématiciens, mal démontrée aussi de mon point de vue. Je veux bien en parler, mais si c'est pour avoir encore une soixantaine de messages d'attaques personnelles tous azimuts, cela ne m'encourage pas trop...

[GaBuZoMeu]

Eh ben, tu en as mis du temps pour répondre à ma question !

Encore de la mauvaise foi. Je dirais plutôt que tu as mis beaucoup de temps à ne pas comprendre ce qu'est la moyenne géométrique.

[Kekia]

Ta blague m'a fait rire de bon cœur GaBuZoMeu et franchement ce n'était pas gagné sur ce fil donc merci à toi.
Ne t'en fais pas, personne ne t'en voudra de ne pas expliquer les ordinaux de Cantor à Spalding.

Pour ton info, c'est moi qui ai liké ton commentaire fatal_error, je l'ai vraiment apprécié, il n'y avait pas un gros suspens sur le déroulé du fil mais c'était bien tenté. Tu noteras j’espère que je suis restée très soft.

[GaBuZoMeu]

sa conception selon laquelle certains nombres infinis ont une valeur cardinale supérieure à d'autres : une conception très contestée par de nombreux mathématiciens

Encore un mensonge. La théorie cantorienne a rencontré pas mal de résistances, c'est vrai. Mais ces résistances portaient sur la considération d'infinis actuels. Maintenant, aucun mathématicien ni aucune mathématicienne ne conteste le fait qu'il y a une floppée de cardinaux infinis. Croire le contraire est une nouvelle preuve d'inculture mathématique.

[Spalding]

Comme je l'ai dit, cette étude sur les nombres arrondis est destinée à améliorer un article Wikipédia. Pour ma question précise, tu m'as juste signalé que c'était en rapport avec la moyenne géométrique, avant ton message in extremis (non lu pour la raison indiquée). Moi, je ne suis pas un mathématicien professionnel. Je me renseigne quand il faut améliorer un article Wikipédia ou pour parler des conceptions de Cantor sur l'infini (après avoir lu un livre à ce sujet). Par contre, je ne vais pas passer des semaines sur la moyenne géométrique. Cela ne vaut pas le coup pour deux lignes tout au plus dans cet article Wikipédia !

S'agissant des ordinaux de Cantor, il s'agit de sa théorie des ensembles dont j'aurais bien parlé. J'allais justement exposer l'originalité des conceptions de Cantor sur l'infini, mais aussi expliquer pourquoi sa conception de nombres infinis cardinaux supérieurs à d'autres est contestable et a d'ailleurs été contestée par des mathématiciens éminents comme Kronecker. Mais avec des dizaines de messages d’attaques personnelles (contre moi ou entre les forumeurs) et des sujets sans arrêt fermés par le modérateur, je suis un peu découragé. On peut me comprendre...

[GaBuZoMeu]

Il te faudrait des semaines pour maîtriser la moyenne géométrique, mais tu es parfaitement à l'aise sur les nombres ordinaux de Cantor. C'est quoi au fait, le livre que tu as lu ?

[Spalding]

Je connais bien les ordinaux de Cantor, dans le cadre de sa théorie des ensembles. Mais je n'avais pas du tout l'ambition d'exposer les conceptions de Cantor dans un simple sujet sur un forum internet (tâche impossible), seulement en donner un aperçu sommaire avant de passer aux sujets de contestation (par des mathématiciens) : en particulier, l'existence de nombres infinis cardinaux supérieurs à d'autres. Cela aurait peut-être donné lieu à une discussion intéressante...

Le livre en question : "Cantor : la formalisation du concept de l'infini", par Gustavo Pineiro (176 pages). Comme ce livre est très cohérent et bourré de références, je suppose que son auteur ne raconte pas n'importe quoi ! Cela dit, il est évident que si je devais écrire une thèse sur Cantor, il faudrait que je lise toutes ses publications (ou presque) en allemand. Pour un simple forum internet, on peut se contenter d'une approche plus légère. Je suis aussi très probablement le seul sur ce forum à avoir lu un livre sur les conceptions de Cantor. Cela me donne donc une certaine autorité pour en parler ici. Mais encore faudrait-il que les forumeurs ne lancent pas des dizaines de messages pour vider leurs querelles personnelles et que le modérateur ne soit pas obligé sans arrêt de fermer des sujets. Alors, je déclare forfait ! Tout le monde pourra le comprendre.

[GaBuZoMeu]

Un livre de vulgarisation, peut-être ni meilleur ni pire qu'un autre. Mais il ne dit sûrement qu'à l'heure actuelle il y a des mathématiciens qui contestent qu'il y a une floppée de cardinaux infinis. Ça, tu l'as révé. La théorie des ensembles, qui est essentiellement une théorie de l'infini, est une théorie mathématique solidement établie, tout à fait respectable et respectée.

Je suis aussi très probablement le seul sur ce forum à avoir lu un livre sur les conceptions de Cantor. Cela me donne donc une certaine autorité pour en parler ici.

Non mais franchement, pour qui te prends-tu ?
Tu es sûrement en tout cas le seul sur ce forum à ne pas savoir ce qu'est une moyenne géométrique.

[Kekia]

Quand je parlais d'ultracrépidarianisme, je ne plaisantais pas malheureusement...

Je te rassure Spalding, tout le monde peut comprendre que tu ne restes parmi nous et on te souhaite une bonne continuation ailleurs (et bon courage aux modérateurs si besoin).

[mathelot]

Bonjour,
quelques infos sur l'infini:

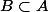déf: Soit un ensemble et une partie propre de A.

A est infini s'il existe une bijection de B sur A.

déf:
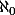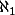On note le cardinal de et le cardinal de et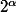
le cardinal de l'ensemble des parties d'un ensemble de cardinal
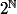le cardinal de R s'appelle la puissance du continu.

théorème de Cantor-Bernstein: soient deux ensembles A et B. S'il existe une application
injective de A dans B et une application surjective de A sur B, alors A et B sont équipotents
(il existe une bijection de A sur B)

Prop: est équipotent à l'ensemble des parties de

déf: l'hypothèse du continu est qu'il n'existe pas de cardinal entre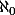 et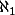
Il me semble que Cohen a montré que cette hypothèse est indémontrable dans l'axiomatique ZF.
l'hypothèse du continu généralisée est que


Remarque: l'axiome du choix permet de travailler avec l'infini. Il est équivalent au fait que toute application surjective admet une application réciproque à droite pour la composition des applications.

[Kekia]

Si vous avec 5min et que le sujet vous intéresse, je conseille cette vidéo relativement tout public de Patrick Dehornoy qui m'avait beaucoup plu sur l'hypothèse du continu https://www.lebesgue.fr/fr/node/4607

[Spalding]

Je vous signale ici que Cantor a été qualifié de charlatan par son contemporain Kronecker, un mathématicien éminent lui aussi, que les conceptions de Cantor ne sont pas bien vues non plus des mathématiciens constructivistes ! Si la théorie des ensembles de Cantor me parait bien démontrée, ce n'est pas du tout le cas pour son postulat de certains nombres infinis cardinaux supérieurs à d'autres !

Comme je l'ai dit, si je devais faire une thèse sur Cantor, il faudrait que je lise toutes ses publications (ou presque) en allemand. GaBuZoMeu l'a-t-il fait ? Si ce n'est pas le cas, il ne doit pas prétendre en savoir plus que moi sur Cantor ! Sur un forum internet, on peut aussi parler de sujets sur lesquels on n'a pas écrit forcément une thèse. Sinon, il n'y aurait presque personne sur ces forums !

Comme je suis très probablement le seul sur ce forum à avoir lu un livre sur les théories de Cantor, je suis le mieux placé pour en parler, davantage en tout cas que GaBuZoMeu (entre nous, il devrait changer son pseudo). Je signale par ailleurs que certains commettent des erreurs grossières sur ce forum (exemples plus haut) !

Mais encore faudrait-il qu'un sujet ne donne pas lieu à un déchaînement de plusieurs dizaines de messages pour vider des querelles personnelles, lesquels messages ont été qualifiés par le modérateur de "déchetterie à ciel ouvert" ! Si le modérateur est aussi obligé de fermer les sujets en question comme cela a été le cas ici, je ne vois pas très bien comment on pourrait avoir une discussion sérieuse.

Avant de créer un autre sujet sur l'infini et Cantor (à condition que le modérateur l'accepte), il faudrait donc que j'aie la certitude qu'il puisse être mené à bien. Seulement, puis-je avoir cette certitude ? Telle est la question !

[fatal_error]

Bonjour

@spalding
tu n'es pas non plus le(la) bienvenue sur maths-forum.

raisons:
pas de changement de comportement
des incessants pavés
que des piques plutot que de se concentrer sur le contenu
le word inchangé avec un potentiel nuisible pour les étudiants

enfin, on sait très bien que cette discussion n'avancera ordinalement que dans son cardinal de message ...

Je ferme et t'invite @spalding à ne pas revenir ici