Inégalité

[chan79]

Bonjour
a, b et c sont trois nombres réels strictement positifs
Montrer que

[Matt_01]

J'ai trouvé en faisant un peu bourrin : on montre que 8abc < (b+c)(a+c)(a+b) .
Quitte à diviser (a,b,c) par a, on peut supposer a=1 et donc montrer 8bc<(b+c)(1+c)(1+b) (c'est là où je fais du bourrin et je calcule un gradient, même si je suis sur qu'avec la bonne inégalité c'est direct).
Avec l'inégalité de la moyenne on montrer alors que la somme des 3 racines est supérieure à 3*(1/8)^(1/6)=3/racine(2) > 2

[chan79]

la somme des 3 racines est supérieure à 3*(1/8)^(1/6)=3/racine(2) > 2

salut
il semble qu'on puisse trouver des valeurs pour a, b et c telles que la somme soit aussi proche de 2 qu'on le veut.
si on prend a=1 et b=c=

la somme est
la limite quand tend vers est 2.
pour a=1 et b=c=25, on arrive à 2,1025...

[Matt_01]

Ouais, j'viens de voir que j'ai écrit une inégalité à l'envers et que du coup c'est n'importe quoi (et j'ai fait les calculs à la va vite, l'histoire du gradient doit être faux).

[Ben314]

J'ai bien une méthode, mais c'est super bourrin....
Comme le truc à minorer est invariant par multiplication de a,b,c par une même constante, on peut supposer sans perte de généralité que a+b+c=1 et il faut donc minorer f(a)+f(b)+f(c) où .

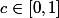
Si on fixe et qu'on cherche le minimum de f(a)+f(b) pour a+b=1-c, cela revient à chercher le minimum de g(x)=f(x)+f(s-x) sur [0,s] (où s=1-c).
Or avec donc
.
Or est négatif en x=0 puis change de signe
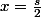
- soit une seule fois en , donc g est croissante puis décroissante donc son minimum est en x=0 et en x=s (on a évidement )
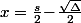
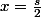
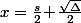
- soit trois fois en ; et donc f est croissante-décroissante-croissante-décroissante et son minimum est soit en x=0 (équivalent à x=s), soit en x=s/2.

Cela signifie que, si on s'autorise les valeurs les valeurs "limites" a=0 ou b=0 ou c=0, le minimum est à rechercher parmi parmi les triplets (1/3,1/3,1/3) ; (1/2,1/2,0) ; (1,0,0) et celui qui donne la plus petite valeur est (1/2,1/2,0) qui donne 2.

EDIT : Et avec une méthode de types gradient, tu risque fortement de te gourer vu que le minimum est atteint au bord du domaine...

[MMu]

Une autre méthode, plus courte et plus accessible au lycée :

Le résultat recherché est immédiat : avec égalité pour
Si on peut facilement généraliser avec égalité pour
............

[chan79]

Une autre méthode, plus courte et plus accessible au lycée :

Bien vu !