Questions de cours sur les lois internes, groupes, anneaux e
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 11 Nov 2009, 16:28
par Timothé Lefebvre » 11 Nov 2009, 16:28
Nightmare a écrit:Quid de l'intersection?
L'intersection de A et B ?
Eh bien je vais essayer de raisonner "naturellement". Si A et B sont des sous-groupes de G, alors leur intersection me donne au minimum e, c'est à dire l'élément neutre de G ? Et au maximum ça devient un réunion et donc G entier ?
Ça me paraît bizarre.
Tu me demandes donc si l'intersection de deux sous-groupes de G est un sous groupe de G.
Dans le cas où l'intersection est minimale je pense que oui puisque on a l'élément neutre. Mais dans le cas où cette intersection est maximale ça me fait pareil qu'une union non ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Nov 2009, 16:31
par Nightmare » 11 Nov 2009, 16:31
Il y a un problème de niveau, le cas de l'intersection est plus simple que celui de la réunion, pas normal que tu bloques sur le premier et pas le second !
Je ne comprends pas ton "au maximum ça devient une réunion" ?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 11 Nov 2009, 16:32
par Timothé Lefebvre » 11 Nov 2009, 16:32
Ben parce que, si l'intersection ne contient qu'un élément c'est le neutre de G, on est d'accord ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Nov 2009, 16:34
par Nightmare » 11 Nov 2009, 16:34
Oui et alors?
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 11 Nov 2009, 16:34
par kazeriahm » 11 Nov 2009, 16:34
L'élément neutre est toujours dans l'intersection de deux sous groupes d'un groupe G.
Essaye de montrer que A inter B est un sous-groupe, et soit tu vas bloquer à un moment, soit ca va marcher.
Prends deux éléments x et y dans A inter B, etc...
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 11 Nov 2009, 16:36
par Timothé Lefebvre » 11 Nov 2009, 16:36
Ah si je sais, je suis con, je peux essayer de faire le même raisonnement, je t'écris ça de suite.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 11 Nov 2009, 16:39
par Timothé Lefebvre » 11 Nov 2009, 16:39
Donc, je reprends A et B des sous-groupes de G.
On a bien A et B qui contiennent le neutre de G, {
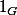
}, puisqu'ils sont sous-groupes de G, donc j'ai
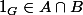
.
Soient a et b dans
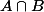
j'ai
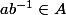
et
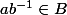
donc
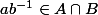
.
Et donc
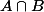
est un sous-groupe de G :id:
Ah, c'est pas dur en fait !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 11 Nov 2009, 16:44
par Nightmare » 11 Nov 2009, 16:44
c'est bien ça !
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 11 Nov 2009, 16:45
par Timothé Lefebvre » 11 Nov 2009, 16:45
En fait il suffit juste de vérifier que les conditions sont bien vérifiées. On applique la définition sans se prendre la tête :)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Nov 2009, 15:12
par Timothé Lefebvre » 12 Nov 2009, 15:12
J'ai fait un schéma très expéditif pour retracer quelques structures algébriques.
Ensemble + lci -> Magma
Magma associatif + élément neutre -> Monoïde
Monoïde + inversibilité de tous les éléments -> Groupe
Groupe + seconde lci -> Anneau
Anneau + tout élément non nul inversible -> Corps
Bien sûr il y a toutes les propriétés qui vont derrière, mais là c'est juste pour avoir une idée générale.
Pouvez-vous confirmer ce schéma ?
Merci.
 par legeniedesalpages » 12 Nov 2009, 15:21
par legeniedesalpages » 12 Nov 2009, 15:21
Timothé Lefebvre a écrit:Groupe + seconde lci -> Anneau
Ce serait plutôt groupe abélien + monoïde + compatibilité entre les deux lois -> anneau
Timothé Lefebvre a écrit:Anneau + tout élément non nul inversible -> Corps
et l'anneau est non réduit à 0 il me semble.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Nov 2009, 15:29
par Nightmare » 12 Nov 2009, 15:29
Remarque, dans un anneau, le groupe additif est forcément abélien.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Nov 2009, 15:29
par Timothé Lefebvre » 12 Nov 2009, 15:29
D'accord, merci de ces précisions, je rajoute ça dans mes notes !
Je vais me lancer dans les exos maintenant ...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Nov 2009, 15:35
par Nightmare » 12 Nov 2009, 15:35
Ma dernière proposition est d'ailleurs un exercice sympathique :happy3:
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 12 Nov 2009, 15:36
par kazeriahm » 12 Nov 2009, 15:36
Comment ca un exercice ?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Nov 2009, 15:38
par Timothé Lefebvre » 12 Nov 2009, 15:38
Oui, celle du polynôme nul, je n'ai pas oublié c'est en cours ;)
Je te dis quand j'ai une piste.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Nov 2009, 15:59
par Nightmare » 12 Nov 2009, 15:59
kazeriahm a écrit:Comment ca un exercice ?
Dans la définition d'un anneau on exige que la loi additive soit commutative. Je dis qu'il est intéressant de montrer qu'en fait elle découle des autres axiomes de la définition.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Nov 2009, 16:00
par Nightmare » 12 Nov 2009, 16:00
Ce n'est pas difficile cela dit, juste amusant.
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 12 Nov 2009, 17:15
par kazeriahm » 12 Nov 2009, 17:15
(G,+) est un groupe abélien. Je considère x une lci associative sur G. Pour être gentil je suppose que x admet un élément neutre (anneau unitaire == anneau selon les définitions, on a déjà abordé la question plus haut). Tu m'affirmes que (G,+,x) est un anneau ? A moins qu'on ne parle pas des mêmes axiomes ?
 par legeniedesalpages » 12 Nov 2009, 17:31
par legeniedesalpages » 12 Nov 2009, 17:31
si j'ai bien compris, l'exo c'est plutôt
(G,+,.) a toutes les propriétés d'un anneau sauf la commutativité de +. Il faut vérifier la commutativité de +.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
