C'est effectivement ce type de constatation qu'il faut faire :
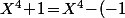\!=\!(X^2\!+\!\alpha)(X^2\!-\!\alpha))
lorsque
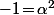
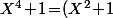^2\!-\!2X^2\!=\!(X^2\!+\!\beta X\!+\!1)(X^2\!-\!\beta X\!+\!1))
lorsque
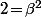
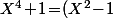^2\!-\!(-2)X^2\!=\!(X^2\!+\!\gamma X\!-\!1)(X^2\!-\!\gamma X\!-\!1))
lorsque
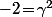
Donc lorsque -1 ou bien 2 ou bien -2 est un carré du corps K le polynôme
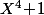
est factorisable (i.e. non irréductible) dans K[X].
or dans Fp, si ni -1, ni 2 ne sont des carré, alors -2 est forcément un carré.
En fait, dans Fp, il n'y a que deux cas de figure :
- Soit un et un seul des trois nombres -1 , 2 , -2 est un carré et une seule des trois décompositions çi dessus est valable et c'est en fait la décomposition de
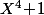
en facteur irréductible.
- Soit les trois nombres -1 , 2 , -2 sont des carrés et dans ce cas il existe

tel que
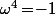
et on a
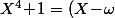(X\!-\!\omega^3)(X\!-\!\omega^5)(X\!-\!\omega^7)=(X\!-\!\omega)(X\!+\!\frac{1}{\omega})(X\!+\!\omega)(X\!-\!\frac{1}{\omega}))
qui, si on regarde les trois façon qu'il y a de regrouper les termes 2 par 2, donnent les 3 factorisation du début de ce post.
EDIT : Si ça t'amuse, montre qu'en fait, quelque soit
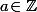
,
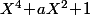
n'est irréductible dans aucun Fp.
Tu peut aussi cherche pour quels

le polynôme
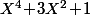
admet il une racine dans Fp.
