[Topologie] Intersection quelconque d'ouverts
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 10 Sep 2018, 09:43
par Sake » 10 Sep 2018, 09:43
Salut,
J'ai un creux, et même si je pense bien avoir fait cet exo en première année de prépa, je me souviens plus d'une astuce...
Il me faut montrer que:
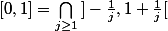
L'inclusion directe est... directe. Mais l'inclusion inverse
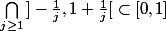
ne me paraît pas immédiate. Je pense avoir lu quelque part qu'il y a un passage à la limite, mais ça me semble bien foireux.
Merci d'éclairer ma lanterne.
Edit : Je tiens à changer "quelconque" par "infinie"
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 10 Sep 2018, 09:53
par Kolis » 10 Sep 2018, 09:53
Bonjour !
Simplement tu montres l'inclusion inverse des complémentaires : si un point n'est pas dans le segment, il n'est pas dans l'intersection, il suffit de prendre un indice assez grand.

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 10 Sep 2018, 10:07
par Sake » 10 Sep 2018, 10:07
Eyy bien vu. Merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Sep 2018, 10:23
par Ben314 » 10 Sep 2018, 10:23
Salut,
Sake a écrit: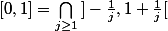
L'inclusion directe est... directe. Mais l'inclusion inverse
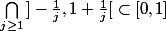
ne me paraît pas immédiate. Je pense avoir lu quelque part qu'il y a un passage à la limite, mais ça me semble bien foireux.
Par "passage à la limite", c'est immédiat : dire que

, ça veut très exactement dire que
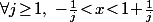
ce qui implique immédiatement que
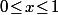
.
(en espérant que tu sait que, si une suite convergente
)
est telle que
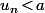
pour tout

, alors la limite est
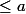
)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 10 Sep 2018, 11:01
par Sake » 10 Sep 2018, 11:01
Voilà, c'est le point qui me posait problème... Pourtant j'ai dû l'apprendre un jour, car il est au programme de TS

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
