Q non intersection d'ouverts de R

[Antho07]

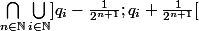
ou la suite (qi)i est la suite indexes de tous les rationnels.

Ce truc a-t-il une chance de valoir Q?

[leon1789]

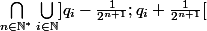
ou la suite (qi)i est la suite indexes de tous les rationnels.

Ce truc a-t-il une chance de valoir Q?

non, ça vaut R : en effet, pour tout n,
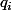
(pour tout entier n, pour tout réel x, on trouve un rationnel tel que )

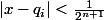
L'idée de Doraki est justement de faire varier l'exposant de 1/2 en fonction de i (pour éviter l'argument ci-dessus), mais cela ne suffit pas encore.

[Antho07]

non, ça vaut R : en effet, pour tout n,

gloups je me suis fait des noeuds dans les indices.



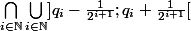
j'ai du mal à visualiser ce que te donne ce truc.

(en faite j'ai vu cela donne l'ensemble vide...)

[yos]

tu étais fatigué hier

Complètement : j'ai dit n'importe quoi. Ton exemple avec R-pi me déprime encore plus alors si tu pouvais cesser.
Ca me heurte : on colle une boule autour de chaque rationnel, lesquels sont denses et pourtant pleins de réels passent à travers.

[leon1789]

gloups je me suis fait des noeuds dans les indices.

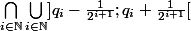
j'ai du mal à visualiser ce que te donne ce truc.
(en faite j'ai vu cela donne l'ensemble vide...)

ben difficile de te confirmer : l'intersection et l'union sont indexées sur la même variable.

[Antho07]

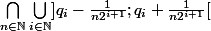
Derniere tentative.....

C'est possible au moins d'écrire Q comme intersection (dénombrable) d'ouverts?

[Dyo]

C'est possible au moins d'écrire Q comme intersection (dénombrable) d'ouverts?

D'ouverts de R, non c'est pas possible, c'est ce qu'il faut montrer en fait ...
:hein:

[yos]

Je tente un raisonnement par l'absurde. Mon idée est d'utiliser la non dénombrabilité de R-Q.
.
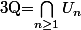
où les sont des ouverts de donc des réunions dénombrables d'intervalles ouverts deux à deux disjoints :
.
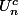
Le complémentaire de ne peut contenir aucun intervalle ouvert (sinon on aurait un rationnel dedans qui ne serait pas adhérent à ). Il ne contient donc qu'un nombre dénombrable de singletons{x}.
Or .
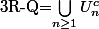
Donc R-Q est dénombrable, ce qui n'est pas.

Je reconnais qu'il y a un passage douteux.

[ThSQ]

Bon une proposition avec Baire pour montrer que c'est pas possible :

Par l'absurde (Léon, fuit pendant qu'il en est encore temps) :

Déjà R\Q est lui intersection dénombrable d'ouverts biscotte Q = réunion de fermés (singletons)

Si Q est l'intersection dénombrable d'ouverts, ces ouverts sont forcément denses (ça a été largement commenté ....).

Si on prend les ouverts pour R\Q et les ouverts pour Q et qu'on en prend l'intersection on a des zouverts denses dont l'intersection est ....... vide en contradiction avec l'ami Bébère.

Edit : les ouvert de R\Q sont denses aussi œuf corse.

[yos]

Déjà R\Q est lui intersection dénombrable d'ouverts biscotte Q = réunion de fermés (singletons)

Si Q est l'intersection dénombrable d'ouverts, ces ouverts sont forcément denses (ça a été largement commenté ....).

Si on prend les ouverts pour R\Q et les ouverts pour Q et qu'on en prend l'intersection on a des zouverts denses dont l'intersection est ....... vide en contradiction avec l'ami Bébère..

Ca me va bien.

[Dyo]

Ok merci à vous !!

[leon1789]

Bien joué :id:
Maintenant que la bataille est terminée, je peux sortir de mon trou pour faire le beau... (je n'ai pas fuit, mais j'étais bien planqué...)

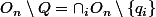
Pour tout ouvert contenant Q (en particulier, dense dans R), est dense dans (Baire), donc dense dans R
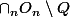
Ainsi est dense dans R (ReBaire)
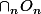
donc est bcp plus gros que Q !!

[leon1789]

Bien joué :id:
(je n'ai pas fuit, mais j'étais bien planqué. Maintenant que la bataille est terminée, je peux sortir de mon trou pour faire le beau... )

Soit des ouverts contenant Q (donc denses dans R).
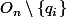
Alors est un ouvert dense également pour tout rationnel .
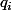
Ainsi est dense dans R, via Baire.
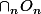
Alors, évidemment est plus gros que Q ... (c'est le moindre que l'on puisse dire !)

Encore une fois, rien d'absurde dans tout ça

[ThSQ]

Encore une fois, rien d'absurde dans tout ça

Encore une fois c'est le raisonnement par l'absurde "retourné" ! :ptdr:

[leon1789]

Encore une fois c'est le raisonnement par l'absurde "retourné" ! :ptdr:

mééé c'est toi qui prends un raisonnement tout simple (que je n'avais pourtant pas trouvé :--: ) pour en faire un truc faisant passer pour "absurde" que est dense, alors que c'est vrai dès que les ouverts contiennent Q... :hum: un tel crime ne devrait pas rester impuni ! :zen:

[ThSQ]

C'est même plus drôle, ça marche à tous les coups :hey: