Implication
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Jan 2007, 22:56
par sue » 07 Jan 2007, 22:56
salut,
j'arrive pas à démontrer cette impliquation :
 (\forall x>\lambda ) \Rightarrow g(x)< 0)
tq :
 = |x|arctan(x) - \frac{\pi}{2}(x-a))
et

prouver l'implication inverse me semble plus facile non ?
MERCI
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Jan 2007, 23:02
par tize » 07 Jan 2007, 23:02
Bonsoir,
en gros tu veux montrer que g est négative sur

pour un certain
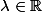
-
mathelot
 par mathelot » 07 Jan 2007, 23:11
par mathelot » 07 Jan 2007, 23:11
ce qui n'a pas l'air d'êtr le cas ...
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Jan 2007, 23:14
par sue » 07 Jan 2007, 23:14
ce qui n'a pas l'air d'êtr le cas ...
je comprend pas g ne peut-elle pas etre négative .. :hein:
sinon Tize , je fais quoi pour le montrer ? je dérive ?
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 07 Jan 2007, 23:28
par dragonmaster » 07 Jan 2007, 23:28
Avec x > 0 , g(x) toujours moins que 0 . (Parce que arctan(x) Il toujours existe

-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Jan 2007, 23:33
par sue » 07 Jan 2007, 23:33
mais il ya

-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 07 Jan 2007, 23:36
par sue » 07 Jan 2007, 23:36
si

je trouve
\in ]-1,1[)
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 08 Jan 2007, 00:35
par dragonmaster » 08 Jan 2007, 00:35
J'ai trompé .
 = arctan(x) + \frac{x}{x^2+1} - \frac{\pi}{2} , x>0)
 =0)
Alors , g est décroissante .
 = a \frac{pi} \geq 0{2})
Alors , avec a>0 , sur une intervalle [k ,

[ , on a g(x) >0 .Il n'existe pas

. Quand a=0 , il existe

-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 08 Jan 2007, 00:36
par dragonmaster » 08 Jan 2007, 00:36
J'ai trompé .
 = arctan(x) + \frac{x}{x^2+1} - \frac{\pi}{2} , x>0)
 =0)
Alors , g est décroissante .
 = a \frac{\pi} {2}\geq 0)
Alors , avec a>0 , sur une intervalle [k ,

[ , on a g(x) >0 .Il n'existe pas

. Quand a=0 , il existe

-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 08 Jan 2007, 00:50
par sue » 08 Jan 2007, 00:50
ok merci mais je comprends pas ou on s'est servi de la condition

?
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 08 Jan 2007, 01:05
par dragonmaster » 08 Jan 2007, 01:05
Si il existe

, on a
0 , sur une intervalle [k,[TEX]+\infty)
[ , g(x)>0
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 08 Jan 2007, 01:30
par sue » 08 Jan 2007, 01:30
ok ok je pige
merci :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités