Démontrer une implication 'Arithmétique'

[raito123]

Bonjours,

Je dois démontrer une implication :

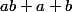
: a^b=1 =>()^()=1

J'ai déja démontrer que pour tout P premier et on a


PS: ^ disigne le PGDC


Quelqu'un a une piste?

Merci pour vos réponses!!

[lapras]

salut,
factorise ton expression a l'intérieur du PGCD et utilise la contraposée de ta proposition que tu as démontré précédement :)

[raito123]

Bonjours Lapras,

En fait ce que tu viens de me dire : je l'ai fait hier et j'ai cru que c'étais juste mais maintenant je pense que ce n'est pas juste car l'expréssion que j'ai démontrer c'est seulement pour les nombres premiers!!

[lapras]

je te montre
on sait que a^b = 1
donc Il n'existe pas P premier divisant ab ET a+b
on suppose que p divise a²b + b²a = ab(a+b)
alors deux cas :
1) p divise ab, p ne divise pas a+b,; donc p ne divise pas ab + a + b
2) p divise a+b : p ne divise pas ab donc p ne divise pas ab + a + b
dans tous les cas il n'existe pas un nombre premier p commun à a+b+ab et a²b + b²a
Si il n'existe aucun nbre premier commun à tes deux nombres, comment veux tu qu'ils aient un diviseur commun qui est soit premier soit composé de nombre premiers

[_-Gaara-_]

:hein2: :hein:

Salut,

Je n'ai rien compris :zen: lol

[raito123]

il n'existe pas un nombre premier p commun à a+b+ab et a²b + b²a

Oui c'est claire je l'ai démontrer aussi mais j'ai oublier la remarque

comment veux tu qu'ils aient un diviseur commun qui est soit premier soit composé de nombre premiers

:++:

[raito123]

Question :

(ab+a+b)^(a²b+ab²) différent de 1 => a^b différent de 1

Est-il juste comme raisonnement pour montrer que :

a^b = 1 => (ab+a+b)^(a²b+ab²) =1

?....

[leon1789]

Bon, je vais mettre mon grain de sel : c'est marrant, la propriété ci-dessous, je l'ai utilisée plusieurs fois ces jours-ci sur le forum, et là encore, elle s'applique pour donner un truc plus fort que ce que demande l'exercice.

Soit , alors divise .

(On peut démontrer ça rapidement, sans raisonnement par l'absurde, sans énumération de cas http://www.maths-forum.com/showpost.php?p=321738&postcount=40)

Appliquer ça deux fois :
-1- avec x=a et y=b : il vient divise
-2- avec x=a+b et y=ab : il vient divise

Conclusion : pour tous entiers a,b , divise

[raito123]

Bon, je vais mettre mon grain de sel : c'est marrant, la propriété ci-dessous, je l'ai utilisée plusieurs fois ces jours-ci sur le forum, et là encore, elle s'applique pour donner un truc plus fort que ce que demande l'exercice.

(On peut démontrer ça rapidement, sans raisonnement par l'absurde, sans énumération de cas http://www.maths-forum.com/showpost.php?p=321738&postcount=40)

Appliquer ça deux fois :
-1- avec x=a et y=b : il vient divise
-2- avec x=a+b et y=ab : il vient divise pgcd(a+b,ab)^2

Conclusion : pour tout entiers a,b , divise

Yep!

La :zen: !!!
________________________________________________________

Tu peux me dire si la relation post n°7 est juste?parce que ça sonne pas bien ?

[leon1789]

j'ai corrigé. merci :)

[raito123]

Tu peux me dire si la relation post n°7 est juste?parce que ça sonne pas bien ?

[leon1789]

Question :

(ab+a+b)^(a²b+ab²) différent de 1 => a^b différent de 1

Est-il juste comme raisonnement pour montrer que :

a^b = 1 => (ab+a+b)^(a²b+ab²) =1

?....

Bien sûr que c'est juste : ça s'appelle le principe de contraposition. :we:
"A => B" est logiquement équivalent à " non B => non A "

Le résultat pgcd(ab+a+b, a²b+ab²) divise pgcd(a,b)^4 implique directement le résultat demandé dans ton exo.

[raito123]

Oui c'est ça!!!!

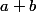
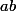
Personnellement, j'ai pris un nombre quelconque d divisant et : c'est toujours possible, quitte à prendre .
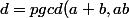Ensuite, grâce à et (exactement le même argument que Rian' !!!), je dis que d divise .

Ainsi, on arrive à cette assertion réutilisable à volonté :
pgcd(a+b, ab) divise pgcd(a,b)²

Maintenant entraine de suite ...

Je n'arrive aps à voir comment tu as fait .

Le résultat pgcd(ab+a+b, a²b+ab²) divise pgcd(a,b)^4 implique directement le résultat demandé dans ton exo.

Oui c'est trés fort!!!

[lapras]

salut,
effectivement tres utile cette proposition !
en plus elle est assez évidente!

[raito123]

Je vois je l'ai trouver!!!!!!

Merci leon1789!!!!!

[yos]

J'ai déja démontrer que pour tout P premier et on a

C'est même équivalent en fait :


Recommence un coup :


C'est ce qu'on veut non?

[lapras]

J'ai une autre maniere de la démontrée
soit d le plus grand diviseur commun à a+b et à ab
alors
ab = 0 [d]
a+b=0[d]
d'où -a² = 0 [d]
donc a² = 0 [d]
de même b²=0[d]
donc d divise a² et d divise b²
donc d est un diviseur commun à a² et b²
donc d divise PGCD(a²;b²)
donc PGCD(a+b , ab) divise PGCD(a;b)²

[raito123]

C'est même équivalent en fait :


Recommence un coup :


C'est ce qu'on veut non?

Si tu veux! Comme départ

J'ai une autre maniere de la démontrée
soit d le plus grand diviseur commun à a+b et à ab
alors
ab = 0 [d]
a+b=0[d]
d'où -a² = 0 [d]
donc a² = 0 [d]
de même b²=0[d]
donc d divise a² et d divise b²
donc d est un diviseur commun à a² et b²
donc d divise PGCD(a²;b²)
donc PGCD(a+b , ab) divise PGCD(a;b)²

:++:

Merci les gars

[leon1789]

J'ai une autre maniere de la démontrée (...)

oui, la congruence permet d'avoir des lignes "légères".

[raito123]

oui, la congruence permet d'avoir des lignes "légères".

Le vocabulaire ça compte pour moi : c'est quoi "les lignes légères"??