Continuités et dérivabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 14 Mai 2018, 17:59
par wilfred1995 » 14 Mai 2018, 17:59
Bonsoir à tous
=\begin{cases}\frac{x}{1+e^{\frac{1}{x}}}<br /> & \text{ si } x\neq0 \\ 0<br /> & \text{ si } x=0<br /> \end{cases})
et
=\begin{cases} x^n\sin{\frac{1}{x}}<br /> & \text{ si } x\neq0 \\ 0<br /> & \text{ si } x=0 <br />\end{cases})
je voulais vérifier si mon cheminement est clair
f est continue si et seulement si la limite de f quand x tend vers 0 et j'ai calculé la limite des deux fonction de f j'ai trouvé 0 j'ai conclu que c'est continue et j'ai fait la même chose avec la dérivabilité et toujours trouver 0 et c'est derivable
Pour la fonction g je suis bloqué au niveau du calcul de la limite quand je varie les n je n'arrive pas à déterminer le général merci.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 14 Mai 2018, 19:53
par pascal16 » 14 Mai 2018, 19:53
pour g.
si n=0 -> elle n'a pas de limite en 0
si n=1 -> la dérivée n'a pas de limite en 0
pour n>1, tu devrais trouver une limite facile avec l'encadrement le plus simple de sin(x)
-
mathelot
 par mathelot » 14 Mai 2018, 20:06
par mathelot » 14 Mai 2018, 20:06
pour n=2, la fonction g est dérivable partout y compris en x=0, mais
la dérivée g' n'a pas de limite quand x tend vers zéro.
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 14 Mai 2018, 20:08
par wilfred1995 » 14 Mai 2018, 20:08
pascal16 a écrit:pour g.
si n=0 -> elle n'a pas de limite en 0
si n=1 -> la dérivée n'a pas de limite en 0
pour n>1, tu devrais trouver une limite facile avec l'encadrement le plus simple de sin(x)
ok j'y réfléchis
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 15 Mai 2018, 20:34
par wilfred1995 » 15 Mai 2018, 20:34
pour n supérieur à 2 je n'arrive pas à canaliser
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 16 Mai 2018, 10:17
par pascal16 » 16 Mai 2018, 10:17
|sin(x)|<= 1
et tu écris la limite du taux d'accroissement
pour n>2, tu as au moins x en facteur et une limite nulle
-
wilfred1995
- Membre Relatif
- Messages: 190
- Enregistré le: 03 Mar 2018, 19:19
-
 par wilfred1995 » 17 Mai 2018, 20:58
par wilfred1995 » 17 Mai 2018, 20:58
Pour
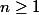
je trouve la limite zéro donc c'est continue.
pour n égal à 0 et 1 elle n'est pas dérivable.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 18 Mai 2018, 08:23
par pascal16 » 18 Mai 2018, 08:23
oui.
c'est une des fonction 'pas gentille'. On a une dérivée de définie, mais pas unee courbe lisse.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 97 invités
