PTSI : Dérivabilité d'une fonction vectorielle
66 messages
- Page 1 sur 4 - 1, 2, 3, 4
PTSI : Dérivabilité d'une fonction vectorielle
Bonjoir,
Je suis en 1ère année de prépa (PTSI) et j'ai un DM de math à rendre pour la rentrée (Donc pas encore pour tout de suite), c'est le dernier exercice qui me pose problème, en effet je n'arrive pas à faire la première question !!! Voici l'énoncé :
Soit deux réels a et c tels que 0 R, t |---> Norme(F1M(t)) est dérivable sur I et calculer sa dérivée.[/B]
Voilà, j'y arrive pas, ça fait 3 jours que je suis dessus sans résultat... Je sais qu'il faut s'inspirer d'un exercice où on savait qu'une fonction vectorielle était dérivable en un point et non-nulle en ce même point, alors sa fonction norme est aussi dérivable... J'aimerais bien faire comme ça, mais il faut d'abord que je prouve que la fonction vectorielle F1M est dérivable sur I, donc que la fonction f est dérivable sur I, et c'est là que ça coince. Une idée ? Ah oui, et il est interdit de passer par les coordonnées !
Merci :we:
Je suis en 1ère année de prépa (PTSI) et j'ai un DM de math à rendre pour la rentrée (Donc pas encore pour tout de suite), c'est le dernier exercice qui me pose problème, en effet je n'arrive pas à faire la première question !!! Voici l'énoncé :
Soit deux réels a et c tels que 0 R, t |---> Norme(F1M(t)) est dérivable sur I et calculer sa dérivée.[/B]
Voilà, j'y arrive pas, ça fait 3 jours que je suis dessus sans résultat... Je sais qu'il faut s'inspirer d'un exercice où on savait qu'une fonction vectorielle était dérivable en un point et non-nulle en ce même point, alors sa fonction norme est aussi dérivable... J'aimerais bien faire comme ça, mais il faut d'abord que je prouve que la fonction vectorielle F1M est dérivable sur I, donc que la fonction f est dérivable sur I, et c'est là que ça coince. Une idée ? Ah oui, et il est interdit de passer par les coordonnées !
Merci :we:
Serru a écrit:
1)On admet pour le moment que Gamma est le support d'un arc C1 (I, f), on a donc Gamma = {M P / Il existe t de I tel que OM=f(t)}
1.1) Montrer que la fonction numérique F1M : I ---> R, t |---> Norme(F1M(t)) est dérivable sur I et calculer sa dérivée.
il faut d'abord que je prouve que la fonction vectorielle F1M est dérivable sur I, donc que la fonction f est dérivable sur I, et c'est là que ça coince. Une idée ?
Bonjour,
si Gamma est le support d'un arc C1 (I, f), cela signifie que la fonction I ---> R, t |--->F1M(t) est de classe C1 sur I.
Donc ton problème est résolu.
Pour que la fonction F1M : I ---> R, t |---> Norme(F1M(t)) soit dérivable sur I, il faut en outre que le vecteur F1M(t) ne s'annule pas, mais c'est la question précédente, n'est-ce pas?
Serru a écrit:C'est ça que ça veut dire, arc C1 ? Je pensais que l'arc était nommé ainsi... ^^"
Dans ce cas, f est dérivable sur I, et F1M = OF1 + F1M, d'où (F1M)' = f'... Ca marche...
J'me sens bête de pas avoir compris, mais merci bien :p
Tu ne pouvais pas deviner si on ne te l'a pas dit.
C0: continue
D1: Dérivable
C1: Dérivable de dérivée continue
D2: Dérivable deux fois
...
Attention, c'est probablement OM = OF1 + F1M.
Ou F1M=F1O+OM
emdro a écrit:Tu ne pouvais pas deviner si on ne te l'a pas dit.
C0: continue
D1: Dérivable
C1: Dérivable de dérivée continue
D2: Dérivable deux fois
...
Attention, c'est probablement OM = OF1 + F1M.
Ou F1M=F1O+OM
Euh oui c'est ça, F1M = F1O + OM = F1O + f, je me suis un peu embrouillé ^^"
En fait je savais ce qu'était une fonction de classe Cn, mais je ne savais pas qu'on parlait d'arcs de classe Cn (En gros, je m'attendais plutôt à ce qu'on me dise "arc (I, f) avec f de classe C1 sur I", j'avais jamais vu cette appellation d'arc C1)
Merci encore :we:
Décidement, ce dernier exercice va me pourrir ma fin de vacances :briques:
Soit deux réels a et c tels que 0 R, t |---> Norme(F1M(t)) est dérivable sur I et calculer sa dérivée.
1.2) En déduire la dérivabilité et la dérivée de la fonction numérique F1M + F2M
1.3) En déduire que pour tout t0 élément de I, M(t0) est un point régulier de Gamma, et que la normale à Gamma en M(to) est la bissectrice intérieure de langle F1-M-F2
Le premier problème réside dans la 1.2), s'agit-il de ||F1M|| + ||F2M|| ou bien de ||F1M + F2M|| ? Je pencherais pour le premier choix mais je n'en suis pas du tout sûr...
Si c'est le 1er, je trouve comme dérivée /||F1M|| + /||F2M||, ce qui colle pas mal car les dénominateurs sont non nuls (F1 et F2 n'étant pas éléments de Gamma).
Si c'est le 2ème, alors j'ai 2/||F1M + F2M||, d'ailleurs je l'aime pas trop celui-là car il n'est pas défini en O...
Ensuite, question 1.3), je dois démontrer que pour tout élément de I, M(t0) est régulier, donc que f' ne s'annule pas sur I... Voilà mon raisonnement :
Par construction de F1 et F2, F1M + F2M = F1O + F2O + 2f = 2f.
D'où 2f'=F1M' + F2M' et 2||f'|| = ||F1M' + F2M'||... Je vois pas le lien avec la question précédente :hein: Quelqu'un peut-il m'apporter son aide ?
Soit deux réels a et c tels que 0 R, t |---> Norme(F1M(t)) est dérivable sur I et calculer sa dérivée.
1.2) En déduire la dérivabilité et la dérivée de la fonction numérique F1M + F2M
1.3) En déduire que pour tout t0 élément de I, M(t0) est un point régulier de Gamma, et que la normale à Gamma en M(to) est la bissectrice intérieure de langle F1-M-F2
Le premier problème réside dans la 1.2), s'agit-il de ||F1M|| + ||F2M|| ou bien de ||F1M + F2M|| ? Je pencherais pour le premier choix mais je n'en suis pas du tout sûr...
Si c'est le 1er, je trouve comme dérivée /||F1M|| + /||F2M||, ce qui colle pas mal car les dénominateurs sont non nuls (F1 et F2 n'étant pas éléments de Gamma).
Si c'est le 2ème, alors j'ai 2/||F1M + F2M||, d'ailleurs je l'aime pas trop celui-là car il n'est pas défini en O...
Ensuite, question 1.3), je dois démontrer que pour tout élément de I, M(t0) est régulier, donc que f' ne s'annule pas sur I... Voilà mon raisonnement :
Par construction de F1 et F2, F1M + F2M = F1O + F2O + 2f = 2f.
D'où 2f'=F1M' + F2M' et 2||f'|| = ||F1M' + F2M'||... Je vois pas le lien avec la question précédente :hein: Quelqu'un peut-il m'apporter son aide ?
Serru a écrit: F1M : I ---> R, t |---> Norme(F1M(t)) est dérivable sur I et calculer sa dérivée.
[B]1.2) En déduire la dérivabilité et la dérivée de la fonction numérique F1M + F2M
s'agit-il de ||F1M|| + ||F2M|| ou bien de ||F1M + F2M|| ? Je pencherais pour le premier choix mais je n'en suis pas du tout sûr...
Bonjour,
quelle est la définition de f+g?
N'est-ce pas t-> f(t)+g(t)?
Alors F1M+F2M:t->F1M(t)+F2M(t)=||F1M|| + ||F2M||, non?
Oui, je suis d'accord, mais là où réside maintenant le problème, c'est que je ne vois pas le rapport enre la dérivée de ||F1M|| + ||F2M|| avec f' (On me demande d'en déduire que M(t0) est régulier pour tout t0 de I), j'ai beau chercher...
Edit : Bon, j'ai trouvé le rapport, si la dérivée de ||F1M|| + ||F2M|| est non nulle, alors nécessairement f' est non nulle. Maintenant, il faut le prouver ! Et... C'est dur !
Edit : Bon, j'ai trouvé le rapport, si la dérivée de ||F1M|| + ||F2M|| est non nulle, alors nécessairement f' est non nulle. Maintenant, il faut le prouver ! Et... C'est dur !
je cherche sur le meme exo que lui :)
apparemment si on a cette derivée non nulle cela veut dire que les deux numérateurs sont non nuls et il y a f' en produit scalaire avec deux vecteurs :
+
probleme bah il y a des denominateurs et je ne vois pas comment montrer que cela ets non nul..(sans passer par les coordonnées)
PS : tu confonds, F1M+F2M = 2a c'est norme(F1M+F2M)
là on a norme de F1M + norme de F2M (pas pareil comme on l'a dit plus haut)
PS2 : chapitre sur les coniques non fait
apparemment si on a cette derivée non nulle cela veut dire que les deux numérateurs sont non nuls et il y a f' en produit scalaire avec deux vecteurs :
probleme bah il y a des denominateurs et je ne vois pas comment montrer que cela ets non nul..(sans passer par les coordonnées)
PS : tu confonds, F1M+F2M = 2a c'est norme(F1M+F2M)
là on a norme de F1M + norme de F2M (pas pareil comme on l'a dit plus haut)
PS2 : chapitre sur les coniques non fait
emdro a écrit:A mon avis, c'est bien de distance(F1M)+distance(F2M) = 2a qu'il s'agit (propriété bifocale de l'ellipse). Et donc ||F1M||+||F2M||.
Mais ça voudrait dire que tout point de l'ellipse est stationnaire ? Ca me semble étrange...
Peut-être doit-on dériver ||F1M + F2M||, mais je ne crois pas...
Flo : J'ai essayé, et un peu qu'y'en a, des racines...
j'étaye le fait que la question me semble impossible à traiter:
Si on considère
x(t)=a*cos(t^3)
y(t)=b*sin(t^3) (b<a)
Pour ceux qui connaissent, c'est l'ellipse de demi grand axe a et de demi petit axe b, mais étrangement paramétrée à dessein.
On a donc F1M+F2M=2a avec F1(-c,0) et F2(c,0), ou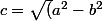) .
.
La fonction f donnée ci-dessus est C1. Pourtant, le point associé au paramètre 0 , n'est pas régulier pour ce paramétrage.
Il est donc faux d'affirmer que tous les points sont réguliers.
Si on considère
x(t)=a*cos(t^3)
y(t)=b*sin(t^3) (b<a)
Pour ceux qui connaissent, c'est l'ellipse de demi grand axe a et de demi petit axe b, mais étrangement paramétrée à dessein.
On a donc F1M+F2M=2a avec F1(-c,0) et F2(c,0), ou
La fonction f donnée ci-dessus est C1. Pourtant, le point associé au paramètre 0 , n'est pas régulier pour ce paramétrage.
Il est donc faux d'affirmer que tous les points sont réguliers.
Serru a écrit:Mais ça voudrait dire que tout point de l'ellipse est stationnaire ? Ca me semble étrange...
Peut-être doit-on dériver ||F1M + F2M||, mais je ne crois pas...
Flo : J'ai essayé, et un peu qu'y'en a, des racines...
Non, pas que tout point est stationnaire, mais que certains peuvent l'être. Attention à la logique!
Et le fait d'être stationnaire dépend du paramétrage choisi.
Si on prend x=a cos(t) et y=b sin(t), il n'y aura pas de point stationnaire, et cela donne la même ellipse.
66 messages
- Page 1 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
