Forum de Mathématiques: Maths-Forum

J'ai un peu de mal à m'exprimer. Je ne parlais naturellement pas d'utiliser un logiciel de CAO ou autre, tout fait, mais de créer des perspectives, non pas avec le coup d'oeil et les capacités artistiques d'un peintre, mais avec les outils modernes que sont les mathématiques, la programmation infor...

Je sais pas ce que tu appelles théorème des dimensions, moi je connais le théorème du rang

Oui, mais justement, on définit cette somme comme la valeur en -1 du prolongement analytique de zeta, qui vaut -1/12

On attribue à cette somme la valeur , où 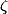est la fonction de Riemann (son prolongement analytique à )

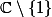Bref, le sens de cette égalité n'est pas intuitif, il faut faire de l'analyse complexe

A ton avis ?
Prend des initiatives

C'est pas trop qu'est-ce que tu as fait ?

Qu'est-ce que tu ne comprends pas, pourquoi card(Q)=card(N) ? c'est juste une notation

En gros ca pose la question de la réversibilité d'un modèle physique donné. Il y a un certain nombres de phénomènes physiques qui sont réversibles (la propagation des ondes par exemple, mais pas la diffusion de la chaleur) : quand on connaît l'état d'un système réversible à un instant T, on peut cal...

Boaf comme tu veux hein, apparement je suis pas le seul à trouver ca ambigu... "on ira à la plage dans 3 ans, lorsque 5 années auront passées" :we: Ce que je veux dire, et après j'arrête de t'embêter avec ca, c'est que c'est dommage d'avoir une ambiguité syntaxique dans un exo de maths, puisque du c...

Attends, dans ce cas c'est moi qui suis dans les choux "L'age du père de ma tante est un nombre premier tel que additionné de 31 on retrouve l'àge de son grand-père et additionné de 27 on retrouve l'àge de sa grand-mère qui ont 140 ans à eux deux. J'interprète ca comme ca : si p est l'age du pe...

ah zut , alors, la deuxième partie était ceci: la tante dans 27 ans aura son propre age actuel 27 ans, donc dans 27 ans elle aura 27+27. ce qui est l'àge du père. la première partie est compréhensible ou pas? "'age du père de ma tante est un nombre premier tel que additionné de 31 on retrouve ...

beagle a écrit:"lorsqu'elle aura vécu le nombre d'année de son age actuel dans 27 ans"

je confirme c'est pas clair du tout, et encore moins une fois que tu as dit que derrière cette phrase se cache le fait que la tante a 27 ans

Archytas a écrit:Et bien la solution positive de l'équation est !

tu ne comprends pas ce que je veux dire

tu as montré que si la suite converge, alors sa limite est solution de x=sqrt(x+9)

mais tu n'as pas montré que la suite convergeait

x=sqrt{9+sqrt{9+sqrt{9+sqrt{9+sqrt{...}}}}}} donc x=sqrt{x+9} ce qui reviens à résoudre une équation du second degré dont la solution positive est la limite de la convergence. Comme pour \phi tss en effet si la suite converge alors elle converge vers x=\sqrt{x+9} mais encore faut-il prouver qu'elle...

Archytas a écrit: converge or donc un converge c'est ça ?

Pourquoi v_n converge ?

Hello

tu as une matrice diagonale

calcule

Bah disons juste que le fait que les algébriques soient dénombrables est moins "célèbre" que son pendant pour les rationnels :we:

En fait ce que tu veux dire c'est que l'ensemble des nombres non transcendants est de mesure nulle, et ce n'est pas évident (à ma connaissance). En revanche le fait que les rationnels soit de mesure nulle est quasi-évident. L'ensemble des nombres algébriques est dénombrable ! Une preuve ici par exe...

D'ailleurs c'est possible de montrer facilement que la probabilité de tomber sur un transcendant en prenant un réel au hasard est de 1 (pour un entier c'est facile de montrer que la proba est 0 mais ça doit être une autre paire de manche pour les irrationnels ^^) ? Je l'avais vu écris sans qu'il y ...

@ptitnoir effectivement en terminale les élèves n'ont pas le bagage pour construire proprement les réels, ni les entiers ou les rationnels d'ailleurs il faut faire un tout petit peu de théorie des ensembles pour ca on se contente de les utiliser (mais tout comme la dérivée ou l'intégrale par exemple)