ok
c'est p+1 pour les deux autres cas
merci raito123 :)
354 résultats trouvés
Revenir à la recherche avancée
- 12 Fév 2012, 21:12
- Forum: ✯✎ Supérieur
- Sujet: Produit de deux séries entières, an?
- Réponses: 6
- Vues: 584
dsl j'ai eu un problème de réseau
entre temps j'ai essayé de raisonner mais bon, je ne vois pas comment on obtient p+1
ce sont peut être les notations, que fait-on du b3p-k?
entre temps j'ai essayé de raisonner mais bon, je ne vois pas comment on obtient p+1
ce sont peut être les notations, que fait-on du b3p-k?
- 12 Fév 2012, 20:38
- Forum: ✯✎ Supérieur
- Sujet: Produit de deux séries entières, an?
- Réponses: 6
- Vues: 584
Bonjour,
Je ne vois pas trop ce qu'il faut faire. Pourriez-vous détailler les étapes?
J'essaierais de le refaire pour les deux autres cas (n=2p+1 et n=2p+2), je ne vois pas du tout comment est-ce qu'on doit raisonner ici.
Je ne vois pas trop ce qu'il faut faire. Pourriez-vous détailler les étapes?
J'essaierais de le refaire pour les deux autres cas (n=2p+1 et n=2p+2), je ne vois pas du tout comment est-ce qu'on doit raisonner ici.
- 12 Fév 2012, 19:13
- Forum: ✯✎ Supérieur
- Sujet: Produit de deux séries entières, an?
- Réponses: 6
- Vues: 584
Produit de deux séries entières, an?
Bonjour,
J'ai f(x) =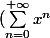(\sum_{n=0}^{+\infty} x^{3n})) .
.
On recherche les coefficients.
J'aimerais comprendre pourquoi si n =3p, = p+1 ?
= p+1 ?
Je sais déjà que:

=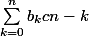
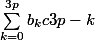
J'ai f(x) =
On recherche les coefficients.
J'aimerais comprendre pourquoi si n =3p,
Je sais déjà que:
=
- 12 Fév 2012, 18:37
- Forum: ✯✎ Supérieur
- Sujet: Produit de deux séries entières, an?
- Réponses: 6
- Vues: 584
- 12 Fév 2012, 10:15
- Forum: ✯✎ Supérieur
- Sujet: rayon de convergence
- Réponses: 8
- Vues: 609
rayon de convergence
Bonjour, je souhaite calculer un rayon de convergence avec: a_n = (\frac{1}{2^n} + \frac{1}{3^n})\frac{1}{n} . En utilisant le critère de d'Alembert, je me suis arrêté à: \frac{3^{n+1} + 2^{n+1}}{6(2^n +3^n)} |x| mais je ne vois pas ce qu'on obtient à l'infini puisqu'on a que des pui...
- 12 Fév 2012, 09:00
- Forum: ✯✎ Supérieur
- Sujet: rayon de convergence
- Réponses: 8
- Vues: 609
seconde inegalité triangulaire
bonjour, j'essaye de redémontrer la seconde inégalité triangulaire, mais j'ai un petit blocage.. on a : ||x|| - ||y|| << ||x-y|| donc en échangeant les rôles de x et y, j'obtiens: ||y|| - ||x|| << ||y-x||. Comment fait-on pour obtenir -||x-y|| << ||x|| - ||y|| ? En utilisant ||y|| - ||x|| << ||y-x||...
- 07 Nov 2010, 13:40
- Forum: ✎✎ Lycée
- Sujet: seconde inegalité triangulaire
- Réponses: 1
- Vues: 1257
- 06 Nov 2010, 13:31
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 8
- Vues: 1971
c'est ce que je trouve aussi, c'est pas moi qui le dit, c'est mon bouquin.
ils disent que la somme avec n variant de 0 à + infini de arctan(1/(n²+n+1)) = pi/2 (c'est pour montrer qu'une série converge..)
ils disent que la somme avec n variant de 0 à + infini de arctan(1/(n²+n+1)) = pi/2 (c'est pour montrer qu'une série converge..)
- 06 Nov 2010, 13:17
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 8
- Vues: 1971
- 06 Nov 2010, 13:09
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 8
- Vues: 1971
si on a arctan(1/n²+n+1) = arctan(n+1) - arctan(n)
on a lim(arctan(n+1) = pi/2 = lim arctan(n) quand n tend vers + infini
donc limarctan(1/n²+n+1) = 0 non?
pourquoi a-t-on limarctan(1/n²+n+1) = pi/2?
on a lim(arctan(n+1) = pi/2 = lim arctan(n) quand n tend vers + infini
donc limarctan(1/n²+n+1) = 0 non?
pourquoi a-t-on limarctan(1/n²+n+1) = pi/2?
- 06 Nov 2010, 13:08
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 8
- Vues: 1971
arctan
bonjour,
quelqu'un peut m'expliquer pourquoi arctan(1/n²+n+1) = arc(n+1) - arctan(n) ? et aussi pourquoi lim(arctan(1/n²+n+²)) = + pi/2?
on a lim arctan(n+1) = pi/2 pour n -> + infini, et lim arctann = + pi/2 aussi pour n -> + inf, pourquoi on a pas une limite nulle merci
quelqu'un peut m'expliquer pourquoi arctan(1/n²+n+1) = arc(n+1) - arctan(n) ? et aussi pourquoi lim(arctan(1/n²+n+²)) = + pi/2?
on a lim arctan(n+1) = pi/2 pour n -> + infini, et lim arctann = + pi/2 aussi pour n -> + inf, pourquoi on a pas une limite nulle merci
- 06 Nov 2010, 12:52
- Forum: ✯✎ Supérieur
- Sujet: arctan
- Réponses: 8
- Vues: 1971
intégrale
Bonjour, j'aimerais savoir pourquoi u -> 1/ u^(alpha) est intégrable sur [lnlna, +infini[, si et seulement si alpha est supérieur à 1? Merci bien
plan orthogonal
bonsoir,je cherche un vecteur appartenant à un "sev" orthogonal au plan d'équation y=xtan(theta), avec theta variant de 0 à pi/2. On me donne la réponse: (-sintheta, costheta,0), mais comment l'obtient-on? merci
- 04 Juin 2010, 21:46
- Forum: ✯✎ Supérieur
- Sujet: plan orthogonal
- Réponses: 1
- Vues: 749
- 23 Mai 2010, 20:35
- Forum: ✎✎ Lycée
- Sujet: norme d'un vecteur
- Réponses: 6
- Vues: 981
- 23 Mai 2010, 20:31
- Forum: ✎✎ Lycée
- Sujet: norme d'un vecteur
- Réponses: 6
- Vues: 981
à chaque fois j'obtiens des résultats comme si j'avais pas de racine (quand j'vérifie avec la correction...)
- 23 Mai 2010, 20:30
- Forum: ✎✎ Lycée
- Sujet: norme d'un vecteur
- Réponses: 6
- Vues: 981
norme d'un vecteur
bonsoir,
comment calcule-t-on déjà la norme d'un vecteur formant une base? (la formule générale)
si j'ai e3= (1,2,-4)can
||e3||= ?
merci
comment calcule-t-on déjà la norme d'un vecteur formant une base? (la formule générale)
si j'ai e3= (1,2,-4)can
||e3||= ?
merci
- 23 Mai 2010, 20:20
- Forum: ✎✎ Lycée
- Sujet: norme d'un vecteur
- Réponses: 6
- Vues: 981
esp. euclidien
Bonsoir,
je ne sais pas comment débuter, une indication svp?
E est un ev. euclidien, et u,v deux vecteurs fixés.
On recherche l'ensemble des x tel que ||u-x||=||v-x|| et l'interprétation géométrique.
merci
je ne sais pas comment débuter, une indication svp?
E est un ev. euclidien, et u,v deux vecteurs fixés.
On recherche l'ensemble des x tel que ||u-x||=||v-x|| et l'interprétation géométrique.
merci
- 18 Mai 2010, 20:14
- Forum: ✯✎ Supérieur
- Sujet: esp. euclidien
- Réponses: 2
- Vues: 597
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
