Forum de Mathématiques: Maths-Forum

Si x=(x_{1}, x_{2}) \in \mathbb C ^{2} alors A \begin{bmatrix} x_{1}\\ \text{} \\ x_{2} \end{bmatrix}=\begin{bmatrix} ax_{1}+b x_{2}\\ \text{} \\ cx_{1}-a x_{2} \end{bmatrix} puis \langle Ax,x\rangle=(ax_{1}+b x_{2})\overline{x_{1}} + (cx_{1}-a x_{2})\overline{x_{2}} Rappelon...

Salut! Pour votre convenance, j'ai ajouté ta condition! Maintenant, SVP donnez moi une réponse ou une piste!

Bonjour! Bien, On sait que le corps des nombres complexes ne peut pas être ordonné. Cette double inégalité signifie que le nombre a est un réel compris entre....... Mais, si vous voulez, je vais modifier le message.!

Salut! Mais un réel est un nombre complexe, non?

Salut tout le monde! J'ai besoin d'aide et je serai reconnaissant pour toute indication. Soit A= \begin{bmatrix} a & b \\ c & -a \end{bmatrix} avec a, b, c des nombres complexes tels que a est un réel avec 0 \leq a <1 et \vert b \vert=1 . Montrer que a^{2}+1\leq 2\sup_{\Vert x \Vert=1} \vert...

SALUT!
Soient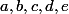 des réels positifs et un réel négatif. Montrer que

Salut abdelmalek.2008
C'est très juste, merci pour la correction.

Pour .
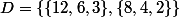, donc , à toi de .......

Salut Ben314: un niveau supérieur pour quelqu'un, c'est lorsqu'on sait pas faire.....

Many tanks to you! Et si tu lisais et non pas Et si tu lisait. il ne vérifierait et non pas il ne vérifierais. les hypothèses et non pas les hypothèse. Je~ crois~ qu'on ~est~ quitte~on~ ce~ qui~ est~ de~ l'information ! Non, je plaisante. Je vous dois beaucoup et merci encore une autre fois.

Soit T un opérateur sur un espace de Hilbert cmplexe H de dimension infinie. On pose W(T)=\{\langle Ax, x\rangle : x\in \B(H), \Vert x\Vert = 1\} et B(T)=\{\langle Ax, x\rangle : x\in \B(H), \Vert x\Vert \leq 1\} . On suppose que 0 \in \sigma(T) \ \ et \ \ \ov...

Merci, bien gagné! mais le lecteur a droit d'une preuve de 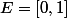et que n'est pas compact ou au moins une référence de ceci!
Et merci encore une fois.

Quant au "théorème" concernant la convergence faible, c'est sûr que je l'ai faussement copié !

Salut, et merci d'avance! Soit H un espace complexe de Hilbert et soient (x_{n}) et (y_{n}) deux suites dans H . On suppose verifiées les deux conditions suivantes: 1) (x_{n}) converge faiblement vers x . ( càd, \langle x_{n},z\rangle converge vers \langle x, z\rangle pour to...

Soit H un espace complexe de Hilbert de dimension infinie. Soit T un opérateur sur H . On pose E=\{<Tx,x>: ~x\in H,~\Vert x\Vert=1\} et F=\{<Tx,x>: ~x\in H,~\Vert x\Vert\leq1\} . On supose que \overline{E} =F , montrer que T est compact. ( \overline{E} désigne l'adhérence de E ).

D'abord je m'excuse beaucoup de ce retard dû à des circonstances personnelles. Quelques définitions: Soit A \in B(H) , le domaine numérique de A est défini comme suit W(A)= \{<Ax,x> : \Vert x \Vert =1 \} Le rayon numérique de A est défini par w(A)=sup \{\vert z\vert ; z\in W&...

Soit un espace de Hilbert complexe. Soit tel que A est normaloide.
Ma question est la suivante:
existe-il un tel que 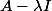soit normaloide?

Soit un compact du plan complexe. Soit le rayon du plus petit disque contenant et
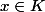=sup { |x-y | : et }.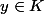

Quelle est la meilleure inégalité qui lie et ?

Salam, Soit B(H) l'algèbre des opérateurs linéaires bornés sur un espace de Hilbert complexe H . Soit K un compact et A \ un élément de \ B(H) \ . On pose \mid K \mid =sup_{B\in K}\parallel B \parallel et on l'appelle module de K . Ma question est la suivante: est ce qu'il existe un ...

Salam,

Ok, et merci.

Compter on commençant par le 1; lorsqu'il qu'il y'a quelque chose à compter sinon vous dites qu'l 'y a "zéro " chose tout simplement !

Tu dois écrire au lieu de