Convergence faible dans un espace de Hilbert

[bagabd]

Salut, et merci d'avance!

Soit un espace complexe de Hilbert et soient et deux suites dans .

On suppose verifiées les deux conditions suivantes:

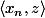
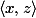
1) converge faiblement vers . ( càd, converge vers pour tout )

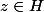
2) converge faiblement vers .

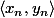
Montrer que converge vers .

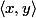
[Ben314]

Salut,
C'est plus que louche ton truc : si c'était vrai, ça signifierais en particulier que, si (xn) est une suite qui converge faiblement vers 0 alors ||xn||²=<xn|xn> tendrait vers <0|0>=0 (en prenant yn=xn dans ton truc) c'est à dire que xn convergerais "normalement" vers 0...