Translaté d'un opérateur normaloide

[bagabd]

Soit un espace de Hilbert complexe. Soit tel que A est normaloide.
Ma question est la suivante:
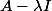
existe-il un tel que soit normaloide?

[aviateur]

Bonjour, c'est bien beau tout ça mais je tombe des nues devant mon ma méconnaissance de ce terme "normaloide."
Il serait bien de définir ce qu'est un opérateur borné normaloide et de même c'est quoi W(A) barre?
Et puis dans le titre pourquoi on a "translaté"?

[aviateur]

Bonsoir
Toujours pas de réponse de @bagdad!! Est ce quelqu'un sait ce qu'est un opérateur normaloide?

[pascal16]

définition via un espace de Hilbert page 13 et 14 :
https://ori-nuxeo.univ-lille1.fr/nuxeo/ ... 8adc1c3c31

par des matrices, page 39, avec un peu de démo dans des cas simples :
https://bu.umc.edu.dz/theses/math/TOU6945.pdf

[aviateur]

Bonsoir
Merci @pascal16 pour les définitions. Il serait bien de temps en temps que lorsqu'on pose une question c'est de rappeler les notions utilisées dans l'exercice qui ne sont pas standard à mon avis (j'entends par là que ce ne sont pas des connaissances de base).
D'après ces définitions on peut voir que s'il existe une base orthogonale de Hilbert qui sont des vecteurs propres de A alors A est normaloide et tout dans W(A) barre (je suppose que le barre ici signifie conjugué et non fermeture) conduit à un opérateur normaloide.
Donc pour poursuivre il faut supposer que A n'est pas diagonalisable. Etant ignorant, je commencerai par étudier la question pour un opérateur en dimension fini avec une seule valeur propre et non diagonalisable. Puis ensuite en utilisant la décomposition de Jordan pour ensuite revenir en dimension infinie.
Mais encore faudrait-il savoir que le posteur réagisse!!

[bagabd]

D'abord je m'excuse beaucoup de ce retard dû à des circonstances personnelles.
Quelques définitions:
Soit , le domaine numérique de est défini comme suit

Le rayon numérique de est défini par
un opérateur est dit normaloide si

Remarques:
1) l'espace de Hilbert est complexe et de dimension infinie.
2) est l'adhérence de .

J'invite les membres et à travailler sur cette question!