Bonjour,
Quelle est la définition d'une fonction surjective?
Quelle est la définition de f(E)?
Merci de ta réponse
578 résultats trouvés
Revenir à la recherche avancée
- 19 Sep 2017, 14:30
- Forum: ✯✎ Supérieur
- Sujet: applications
- Réponses: 2
- Vues: 280
Re: Limites de fonction
Salut, J'ai l'impression que ton problème revient à calculer les limites en 0, et + \infty de la fonction Arctan. Tu les connais? Sinon tu peux aller tapper arctan sur google et n'importe quelle page fera l'affaire je pense. Si jamais tu les connais, peux tu utiliser les règles usuelles sur les limi...
- 13 Fév 2017, 18:16
- Forum: ✯✎ Supérieur
- Sujet: Limites de fonction
- Réponses: 3
- Vues: 321
Re: (Prépa ECE) Suites matricielles et factorielles.
Ouais fait gaffe c'est pas une matrice colonne à deux entrées mais un coefficient binomial, qu'on note comme ça. Je te suggère de lire les quelques lignes du wiki si tu n'as jamais croisé cet animal avant.
https://fr.wikipedia.org/wiki/Coefficient_binomial
https://fr.wikipedia.org/wiki/Coefficient_binomial
- 18 Jan 2017, 16:21
- Forum: ✯✎ Supérieur
- Sujet: (Prépa ECE) Suites matricielles et factorielles.
- Réponses: 8
- Vues: 854
Re: (Prépa ECE) Suites matricielles et factorielles.
Quelle était ta définition? J'en suis curieux
- 18 Jan 2017, 16:11
- Forum: ✯✎ Supérieur
- Sujet: (Prépa ECE) Suites matricielles et factorielles.
- Réponses: 8
- Vues: 854
Re: (Prépa ECE) Suites matricielles et factorielles.
Salut,
Peux-tu donner la définition de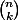 ? (Avec des factoriels)
? (Avec des factoriels)
Peux-tu donner la définition de
- 18 Jan 2017, 16:05
- Forum: ✯✎ Supérieur
- Sujet: (Prépa ECE) Suites matricielles et factorielles.
- Réponses: 8
- Vues: 854
Re: Fourier et Steinhaus
Cool! ouais on progresse bien avec Ben 
- 16 Nov 2016, 17:11
- Forum: ✯✎ Supérieur
- Sujet: Fourier et Steinhaus
- Réponses: 13
- Vues: 608
Re: Fourier et Steinhaus
Salut Lostounet! Ouais ça fait pas mal de temps, j'ai un peu délaissé le forum mais je compte bien y revenir!
Je démarre ma thèse cette année .
.
et toi?
Je ne t'avais pas oublié non plus
Je démarre ma thèse cette année
et toi?
Je ne t'avais pas oublié non plus
- 16 Nov 2016, 15:19
- Forum: ✯✎ Supérieur
- Sujet: Fourier et Steinhaus
- Réponses: 13
- Vues: 608
Re: Fourier et Steinhaus
T'inquiètes on est beaucoup à raisonner avec des gentils convexes compacts parce que c'est plus visuel 
- 16 Nov 2016, 14:17
- Forum: ✯✎ Supérieur
- Sujet: Fourier et Steinhaus
- Réponses: 13
- Vues: 608
Re: topologie :
Oui j'avais pas bien vu la premiere intersection: il y'avait l'adhérence de A...
- 16 Nov 2016, 14:16
- Forum: ✯✎ Supérieur
- Sujet: topologie :
- Réponses: 27
- Vues: 1055
Re: topologie :
Dans le 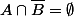 c'est pas plutot:
c'est pas plutot: 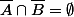 ? Sinon je vois pas comment A est fermé
? Sinon je vois pas comment A est fermé
- 16 Nov 2016, 12:08
- Forum: ✯✎ Supérieur
- Sujet: topologie :
- Réponses: 27
- Vues: 1055
Re: exemple d(x,F)= 0 mais x n'est pas dans F
Salut. Du coup dans un premier temps tu cherches un sous-espace non fermé d'un espace pré-hilbertien. Tu sais peut être qu'un hyperplan est fermé ssi il est le noyau d'une forme linéaire continue? Dans ce cas comment obtenir un hyperplan non fermé? (qui sera même dense!) Edit: Pardon Ben j'avoue ne ...
- 16 Nov 2016, 12:00
- Forum: ✯✎ Supérieur
- Sujet: exemple d(x,F)= 0 mais x n'est pas dans F
- Réponses: 3
- Vues: 573
Re: Un probleme de compacité
Salut. Ton ensemble ça reste bien une partie fermée bornée dans un espace de dimension finie non? (c'est inclus dans la boule que tu as donnée plus bas)
- 26 Mai 2016, 22:47
- Forum: ✯✎ Supérieur
- Sujet: Un probleme de compacité
- Réponses: 5
- Vues: 544
Re: Serie de Fourier
Salut.
Il y'a un théorème bien précis qui permet de donner la convergence uniforme d'une série de fourier suivant la régularité de la fonction. Ca te dit quelque chose?
Sinon t'es sur de ta série? Pour moi la fonction n'est pas impaire, donc la série ne doit pas l'être non plus
Il y'a un théorème bien précis qui permet de donner la convergence uniforme d'une série de fourier suivant la régularité de la fonction. Ca te dit quelque chose?
Sinon t'es sur de ta série? Pour moi la fonction n'est pas impaire, donc la série ne doit pas l'être non plus
- 11 Mai 2016, 13:52
- Forum: ✯✎ Supérieur
- Sujet: Serie de Fourier
- Réponses: 2
- Vues: 411
Re: Problème polynômes, Applications linéaires, matrices
Bah une fois qu'on connait le degré d'un polynome et que celui ci est assez petit, on peut se permettre la résolution d'un système linéaire à la main, et je vois pas le rapport entre résoudre cette question et donner la matrice de l'application linéaire donnée. Dans tous les cas c'est un exo d'algèb...
- 23 Fév 2016, 17:11
- Forum: ✯✎ Supérieur
- Sujet: Problème polynômes, Applications linéaires, matrices
- Réponses: 56
- Vues: 2485
Re: Problème polynômes, Applications linéaires, matrices
ce que dit Robot m'a pourtant l'air le plus simple et le plus approprié à la question. Je ne vois pas en quoi la démarche proposée répond aux questions 2 et 3? Pour reprendre ce que dit Robot, concentre toi uniquement sur le coefficient dominant d'un polynôme qui vérifie ça. Quelle est la relation v...
- 23 Fév 2016, 16:48
- Forum: ✯✎ Supérieur
- Sujet: Problème polynômes, Applications linéaires, matrices
- Réponses: 56
- Vues: 2485
Re: Pari hasardeux.
Rebonsoir. Décidément je ne vais plus trop sur ce forum... Faut que je m'y ré-acclimate! Je suis heureux d'avoir ressorti un vieux trésor :). Personnellement je l'ai trouvé vraiment joli et sa solution élégante, surtout en se faisant guider lentement vers la solution comme l'a fait fahr dans son pos...
- 22 Fév 2016, 19:06
- Forum: ⚔ Défis et énigmes
- Sujet: Pari hasardeux.
- Réponses: 17
- Vues: 844
Pari hasardeux.
Bonsoir tout le monde! Je reviens vers vous après une petite absence avec une enigme rigolote. Je vais essayer d'être le plus limpide possible dans l'énoncé. On considère 100 personnes (ou n pair assez grands) numérotés de 1 à 100. Ils entrent dans une salle dans laquelle il y'a 100 boites. Chacun d...
- 17 Fév 2016, 19:10
- Forum: ⚔ Défis et énigmes
- Sujet: Pari hasardeux.
- Réponses: 17
- Vues: 844
- 03 Jan 2016, 21:09
- Forum: ✯✎ Supérieur
- Sujet: Primitive
- Réponses: 1
- Vues: 282
Et si tu tracais la fonction partie entière sur un papier, et essayais de calculer l'air de la courbe sur la surface?
- 03 Jan 2016, 15:07
- Forum: ✯✎ Supérieur
- Sujet: Integration (SIMPLE)
- Réponses: 28
- Vues: 1236
- 01 Jan 2016, 16:16
- Forum: ⚔ Défis et énigmes
- Sujet: inégalité pas trop difficile
- Réponses: 6
- Vues: 1022
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
