Integration (SIMPLE)
29 messages
- Page 1 sur 2 - 1, 2
Integration (SIMPLE)
Bonjour, je n'arrive pas à cet exercice :
Pour tout couple d'entiers naturels (p,n) tels que p<= n, calculer :
intégralle de p à n de la partie entière de x (dx)
(Je n'arrive pas à utiliser le format mathématiques...)
Merci d'avance
Pour tout couple d'entiers naturels (p,n) tels que p<= n, calculer :
intégralle de p à n de la partie entière de x (dx)
(Je n'arrive pas à utiliser le format mathématiques...)
Merci d'avance
Contexte : 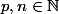 tels que
tels que 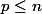 ;
; 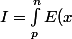 \ {\rm d}x) .
.
Salut !
En remarquant que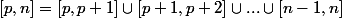 , que vaut
, que vaut ) lorsque :
lorsque :
- appartient à
appartient à 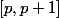 ?
?
- appartient à
appartient à 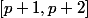 ?
?
...
- appartient à
appartient à 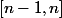 ?
?
Déduis-en ainsi la valeur de \ {\rm d}x) sachant que :
sachant que :
[CENTER] \ {\rm d}x + \int_{p+1}^{p+2} E(x) \ {\rm d}x + ... + \int_{n-1}^n E(x) \ {\rm d}x = \int_p^n E(x) \ {\rm d}x) [/CENTER]
[/CENTER]
:+++:
Salut !
En remarquant que
-
-
...
-
Déduis-en ainsi la valeur de
[CENTER]
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Tu n'as pas besoin de primitiver : rappelle-toi que la fonction partie-entière est une fonction constante par intervalles ou en escalier
capitaine nuggets a écrit:que vautlorsque :
-appartient à
?
-appartient à
?
...
-appartient à
?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Revois la définition de la partie entière pour mieux comprendre.
Prenons par exemple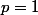 et
et  ; si
; si 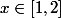 , alors
, alors ) est une constante et vaut ?
est une constante et vaut ?
(et l'intégrale d'une fonction constante étant facile à calculer, on n'a pas besoin de primitiver).
Plus généralement, si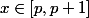 , alors que vaut
, alors que vaut ) ?
?
:++:
Prenons par exemple
(et l'intégrale d'une fonction constante étant facile à calculer, on n'a pas besoin de primitiver).
Plus généralement, si
:++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
KUIP32 a écrit:E(x) vaut p ?
Mais cela n'a aucune importance puisqu'il ne s'agit que d'un singleton de l'intervalle, je m'explique :
[CENTER]
(en gros, si tu enlèves un singleton, tu ne changes pas la valeur de l'intégrale).
Je te laisse poursuivre.
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Oui, il va falloir faire une somme :
capitaine nuggets a écrit:que vautlorsque :
-appartient à
?
-appartient à
?
...
-appartient à
?
Déduis-en ainsi la valeur desachant que :
[CENTER][/CENTER]
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Je ne comprends pas.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Avec la relation de Chasles :lol3:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
29 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
