3660 résultats trouvés
Revenir à la recherche avancée
- 31 Mar 2015, 07:52
- Forum: ✯✎ Supérieur
- Sujet: Quotient algèbre symétrique et algèbre extérieure
- Réponses: 17
- Vues: 2134
- 31 Mar 2015, 07:38
- Forum: ✯✎ Supérieur
- Sujet: operateur adjoint
- Réponses: 6
- Vues: 1003
Je pense pas. Par exemple si tu prends une matrice n*n, son adjoint est la transposée, qui a toujours même spectre.
- 29 Mar 2015, 14:36
- Forum: ✯✎ Supérieur
- Sujet: operateur adjoint
- Réponses: 6
- Vues: 1003
Peut être que tu veux dire : le groupe engendré par les transpositions. Mais ce groupe n'est pas très intéressant...
- 31 Déc 2014, 14:12
- Forum: ✯✎ Supérieur
- Sujet: quotient
- Réponses: 10
- Vues: 719
Juste pour rappeler un théorème connu sur un corps k : toute variété abélienne est semi-simple (à isogénie près) , i.e. produit de variété abéliennes irréductibles (qui ne possèdent pas de sous-variétés abéliennes). Je ne sais pas si on peut dire que "génériquement" une variété abélienne est irréduc...
- 28 Oct 2014, 23:12
- Forum: ⚜ Salon Mathématique
- Sujet: A propos des variétés abéliennes
- Réponses: 12
- Vues: 1146
C'est bon j'ai trouvé l'erreur. Dans la fonction de droite avec les Bernoulli, je compte plusieurs fois les mêmes coefficients de Fourier. Par exemple, pour m=n, il y a un terme (-1)^m/mn qui provient du cas mn(m-n) != 0 que je traduit par B1(x+1/2)B1(y)-B1(x)B1(y), mais ça donne un coefficient de F...
- 27 Oct 2014, 16:21
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
3) Oui : un produit de courbes elliptiques. Sinon les exemples les plus intéressants sont obtenus en prenant la Jacobienne d'une courbe (exemple : les courbes modulaires). Une forme modulaire donne naissance à une variété abélienne avec beaucoup d'endomorphismes (les opérateurs de Hecke). Cette vari...
- 27 Oct 2014, 00:54
- Forum: ⚜ Salon Mathématique
- Sujet: A propos des variétés abéliennes
- Réponses: 12
- Vues: 1146
Je n'arrive pas à avoir un graphe dynamique avec Sage (à cause d'un problème de Java...).
Mais j'ai une image statique :

Si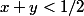 la fonction de droite (avec les Bernoulli) vaut
la fonction de droite (avec les Bernoulli) vaut 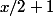 .
.
Mais j'ai une image statique :

Si
- 25 Oct 2014, 23:16
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
Ce n'est pas si louche que ça. Par exemple en une dimension, la fonction 2(B_1(x)-B_1(x+\frac{1}{2})) vaut -1 sur ]0,\frac{1}{2}[ et 1 sur ]\frac{1}{2},1[ . Donc tu peux obtenir des fonctions indicatrices facilement avec des fonctions polynomiales de Bernoulli. Pour ce qui es...
- 25 Oct 2014, 22:01
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
ça fait plusieurs jours que je suis sur un calcul paradoxal (deux fonctions qui ont les mêmes coefficients de Fourier mais différentes, et j'ai fait attention aux coefficients exceptionels), impossible de comprendre où est l'erreur. Considérons la fonction f : \mathbb{R}^2 \rightarrow \mathbb{R} tel...
- 25 Oct 2014, 14:20
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
- 23 Oct 2014, 09:42
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
Merci beaucoup Ben ! (la vérification par ordinateur était numérique : j'ai vérifié pour quelques c_(m,n) que l'intégrale donnait bien ce que je voulais, avec mn !=0 puis avec m=0 ou n=0).
- 20 Oct 2014, 19:50
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
Je ne vois pas où tu veux en venir : je n'ai pas besoin de passer aux étapes ii) et iii). En effet il devrait y avoir une erreur de calcul, mais je ne la vois pas (comme je l'ai déjà dit, j'ai même vérifié ceci à l'ordinateur).
- 18 Oct 2014, 10:45
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
- 18 Oct 2014, 10:36
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
Je ne comprends pas ta réponse. Si j'ai une fonction L^1 et L^2, je peux définir ses coefficients de Fourier (juste avec une intégrale). Cela induit une injection isométrique dans l'espace des suites (ici à deux indices) L^2. Encore une fois, je n'ai jamais prétendu sommer la "série de Fourier". Je ...
- 18 Oct 2014, 10:31
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
Merci pour ta réponse. Attention, je n'ai jamais écrit que je sommais quoi que ce soit. Je dis juste qu'une fonction dont les coefficients de Fourier sont nuls a pour norme L^2 zéro, donc est presque partout nulle. Je n'ai pas l'impression d'avoir fait une erreur de calcul : j'ai même vérifié le cal...
- 18 Oct 2014, 10:23
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
Coefficients de Fourier : paradoxe ?
Bonjour, j'ai un problème qui semble paradoxal qui intervient quand j'essaie d'écrire la fonction min(x,y) en série de Fourier. Je n'ai pas fait d'analyse depuis longtemps, donc il se peut que ça soit trivial. Considérons la fonction f : \mathbb{R}^2 \rightarrow \mathbb{R} donnée sur ]0,1[^2...
- 17 Oct 2014, 20:50
- Forum: ✯✎ Supérieur
- Sujet: Coefficients de Fourier : paradoxe ?
- Réponses: 20
- Vues: 2640
- 23 Sep 2014, 10:09
- Forum: ✯✎ Supérieur
- Sujet: Série harmonique non entière
- Réponses: 10
- Vues: 1641
- 22 Sep 2014, 10:15
- Forum: ✯✎ Supérieur
- Sujet: Série numérique
- Réponses: 9
- Vues: 795
En fait, pour calculer cette intégrale, il suffit de trouver une primitive évidente : \frac{1}{1-\alpha}F(t)^{1-\alpha} . Du coup l'analogue discret est de poser V_n = \frac{1}{1-\alpha}S_n^{1-\alpha} . Calcule alors V_{n+1}-V_n . L'exo en continue en lui même ne résout pas l'exercice, mais ...
- 21 Sep 2014, 21:37
- Forum: ✯✎ Supérieur
- Sujet: Série numérique
- Réponses: 9
- Vues: 795
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
