Inégalité

par **nee-san** » 24 Déc 2010, 20:06

:hum: bonjour à tous, alors j'aurai des questions portant sur un même sujet:les inégalité.

1)quel sont les inégalité principale à connaitre en général et pour les olympiade
2)auriez vous des sites autre que animath pour apprendre les bases.
3)comment procéder vous pour prouver une inégalité type olympiade par exemple ou celles ou l'on a des conditions(du genre a+b+c=1).

jespère ne pas vous déranger et je remercies ce qui prendrons le temps de me répondre

par **Olympus** » 25 Déc 2010, 13:21

Salut !

1) Cela dépend des goûts, mais je dirais AM-GM, Schur, Jensen, Cauchy-Schwarz/Hölder et Tchebyshev .

2) Euh pour les bases, y quand même pas mieux que le poly d'Animaths ! Y a un autre .pdf de Hojoo Lee en anglais mais je ne le retrouve plus, sinon il est quand même d'un niveau plus haut ( même s'il prétend s'adresser aux débutants ) que celui d'Animath . En gros, commence par le poly d'Animaths, fini les chapitres sur les inégalités précédemment citées et ne te préoccupe pas d'autres documents pour le moment ;-)

3) Ben ces conditions peuvent aider à "homogénéiser" l'inégalité, c'est à dire mettre tous les termes au même degré . Par exemple, avec a+b+c=1, si un terme

est au degré 2 ( c'est à dire que

) et que tous les autres sont au degré 5, tu le multiplies par

sans que le résultat ne change, car

.

On peut aussi procéder à un changement de variables pour homogénéiser .

Par exemple, si on a

avec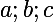

des réels strictement positifs, alors il existe un triplet de réels strictement positifs

tels que

.

Une fois fait ce changement de variables, ton inégalité devient automatiquement homogène en x, y et z !

Preuve : il suffit de prendre

. On vérifie alors aisément que

Si on a maintenant

:

Mais selon la précédente substitution :

Où

Après, y a d'autres moyens de substitution, comme les substitutions trigonométriques par exemple . Mais bon, pour le moment, si tu débutes, ça sert à rien d'avoir un gros sac de substitutions ^^ L'astuce du a+b+c=1 ou abc=1 te suffira amplement pour le moment .

par **nee-san** » 25 Déc 2010, 20:18

ok merci pour ta réponse très détailler mais j'ai des souci principaux:
1) ça veut dire que d'une inégalité est homogène
2)comment tu sais quand il faut utiliser am-mg ou je sais pas quoi
3)si j'ai une inégalité et que j'utilise am-gm,je fait comment pour savoir à quel n je l'utilise
4)j'ai pas compris le principe des inégalité,genre quand je voie des inégalité ou vous utiliser une inégalité connue comment tu peu conclure pour dire que la première est bonne

par **Olympus** » 25 Déc 2010, 20:26

Pour la 1), comme je l'ai dit, on dit qu'une expression est homogène si tous ses termes sont au même degré . Par exemple

est homogène en a, b et c car tous ses termes sont au degré 2 . Par contre,

ne l'est pas, car les termes "a" et "b" y sont au premier degré, alors que "abc" est au troisième degré .

Pour les 2) et 3), ça vient avec l'expérience et un peu d'intuition . À force de faire et refaire des exos, tu peux acquérir les réflexes que tu recherches .

Pour la 4), je n'ai pas compris ta question .

par **nee-san** » 25 Déc 2010, 20:29

Olympus a écrit:Pour la 1), comme je l'ai dit, on dit qu'une expression est homogène si tous ses termes sont au même degré . Par exemple est homogène en a, b et c car tous ses termes sont au degré 2 . Par contre, ne l'est pas, car les termes "a" et "b" y sont au premier degré, alors que "abc" est au troisième degré .

Pour les 2) et 3), ça vient avec l'expérience et un peu d'intuition . À force de faire et refaire des exos, tu peux avoir les réflexes que tu recherches .

Pour la 4), je n'ai pas compris t'as question .

encore merci de tes réponse, alors je vais reformulée ma quatrième question pour la rendre compréhensible.Je voulais savoir quand on à une inégalité, et que j'utile AM-GM par exemple,je tombe sur une inégalité différente de celle qui était demander à démontrer alors comment on peut arriver à conclure que la première est vrai

par **nathanap** » 25 Déc 2010, 20:34

bah tu sais quand même comment on démontre une inégalité en mathématiques ?? c'est de la logique :s

par **nee-san** » 25 Déc 2010, 20:38

nathanap a écrit:bah tu sais quand même comment on démontre une inégalité en mathématiques ?? c'est de la logique :s

soit je comprend que ce soit de la logique, mais j'arrive pas à comprendre genre dans une inégalité ou j'utilise AM-GM je trouve un truc différent de la première inégalité donc je comprend pas le rapport avec la première

par **nathanap** » 25 Déc 2010, 21:05

bah après c'est pas parce que tu utilises une inégalité connue sur un des deux membres que tout va forcément se débloquer, ce serait trop facile
tu peux donner cet exemple ?

par **nee-san** » 25 Déc 2010, 21:06

nathanap a écrit:bah après c'est pas parce que tu utilises une inégalité connue sur un des deux membres que tout va forcément se débloquer, ce serait trop facile
tu peux donner cet exemple ?

j'ai mais franchement rien compris :cry:

par **Olympus** » 25 Déc 2010, 21:23

Je crois savoir d'où vient le problème . Tu crois peut-être qu'il suffirait d'appliquer bêtement les inégalités précédemment citées pour avoir directement le résultat recherché ... Sauf que, tout d'abord, tu dois bien appliquer le théorème en question avec un choix judicieux des variables ( sinon tu tombes sur des inégalités pas assez fortes pour impliquer celle qui est à prouver ) . Et pour ça, comme je te l'ai déjà dit, il faut faire et refaire pas mal d'exos pour avoir une certaine intuition .

Regarde par exemple mon premier post dans ce thread : http://www.maths-forum.com/toujours-inegalites-114768.php . Le choix des variables sur lesquelles j'ai appliqué AM-GM n'est pas vraiment évident . C'est ce genre de choix "astucieux" dont je parle => y a pas de règle générale, cela vient avec l'intuition et l'expérience ( comprendre faire et refaire des exos ) .

Puis, une fois obtenu une inégalité assez forte, tu te débrouilles avec tes capacités de raisonner pour en déduire l'inégalité recherchée .

par **nee-san** » 25 Déc 2010, 21:30

Olympus a écrit:Je crois savoir d'où vient le problème . Tu crois peut-être qu'il suffirait d'appliquer bêtement les inégalités précédemment citées pour avoir directement le résultat recherché ... Sauf que, tout d'abord, tu dois bien appliquer le théorème en question avec un choix judicieux des variables ( sinon tu tombes sur des inégalités pas assez fortes pour impliquer celle qui est à prouver ) . Et pour ça, comme je te l'ai déjà dit, il faut faire et refaire pas mal d'exos pour avoir une certaine intuition .

Regarde par exemple mon premier post dans ce thread : http://www.maths-forum.com/toujours-inegalites-114768.php . Le choix des variables sur lesquelles j'ai appliqué AM-GM n'est pas vraiment évident . C'est ce genre de choix "astucieux" dont je parle => y a pas de règle générale, cela vient avec l'intuition et l'expérience ( comprendre faire et refaire des exos ) .

Puis, une fois obtenu une inégalité assez forte, tu te débrouilles avec tes capacités de raisonner pour en déduire l'inégalité recherchée .

ah d accord donc faut que je m'emtrainé et genre quand j'utiliserai par exemple

avec une certaine variable je tomberai sur un truc qui ressemble à la première inégalité et en raisonnent dessus j'arriverai à conclure.et j'ai vue le sujet que ta résolus je me demande si tes humains à sortir des truc comme ça va me falloir des siècle pour faire ça

par **nathanap** » 26 Déc 2010, 14:20

nee-san a écrit:ah d accord donc faut que je m'emtrainé et genre quand j'utiliserai par exemple avec une certaine variable je tomberai sur un truc qui ressemble à la première inégalité et en raisonnent dessus j'arriverai à conclure.et j'ai vue le sujet que ta résolus je me demande si tes humains à sortir des truc comme ça va me falloir des siècle pour faire ça

oui j'ai lu quelques sujets sur le forum, il résout presque toutes les inégalités qui sont proposées

au fait olympus tu passes les olympiades cette année ?

sinon nee-san, dis toi qu'en plus d'avoir de l'expérience il faut de la patience, dans le système scolaire on t'apprend à ne passer que quelques minutes sur chaque question dans un devoir, mais en maths il y a des problèmes qui demandent plus de temps pour être résolus, en particulier les exercices d'olympiades peuvent nécessiter plusieurs heures.
Quand tu regardes un sujet d'olympiade, chacun des deux sujets comporte 3 exercices et s'étale sur 4 heures et demi, et en général les candidats ne touchent pas à tous les exos; donc ca laisse le temps

par **Olympus** » 26 Déc 2010, 14:50

nathanap a écrit:au fait olympus tu passes les olympiades cette année ?

Non, j'ai déjà pris ma retraite après avoir été premier de ma région l'année dernière :king:

par **nee-san** » 26 Déc 2010, 15:24

ok merci pour vos réponse très détailler à vous deux

par **Olympus** » 26 Déc 2010, 16:37

Un petit HS, @nee-san : ta boîte mp est pleine ^^"

par **nee-san** » 26 Déc 2010, 18:49

Olympus a écrit:Un petit HS, @nee-san : ta boîte mp est pleine ^^"

ah merci de l'info je les vider un peu

Inégalité

inégalité

Qui est en ligne