Bonsoir, petite question sur un exercice.
Soit une suite u définie par
U(n+1)=(-1)^n × cos(U(n-1))/n
Et Uo un réel
J'ai déjà montré que Un-->0 et que Un est équivalent à (-1)^n /n
Bien que la série de terme général (-1)^n /n converge on ne peut rien dire sur la série se terme générale Un car l'équivalent n'est pas une suite à Termes positifs.
Je n'arrive pas à montrer proprement la convergence de la série de terme général Un
Un peu d'aide serait la bienvenue
Séries numériques
4 messages
- Page 1 sur 1
Re: Séries numériques
Bonsoir,
on a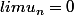 quand n tend vers l'infini et
quand n tend vers l'infini et 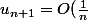)
Faire un développement limité de) à l'ordre 2
à l'ordre 2
on a
Faire un développement limité de
Re: Séries numériques
Bonjour,
^n}{n} cos(u_{n-1}))
en faisant un développement limité:
^n}{n} \left(1-\dfrac{1}{2}u_{n-1}^2+o(u_{n-1}^2) \right))
or:
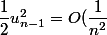)
et
=o(\dfrac{1}{n^2}))
La série de terme général u_n est donc la somme d'une série alternée, convergente mais non absolument convergente, et d'une série absolument convergente.
Pour les notations "o" et "O" de Landau , voir ci-dessous:
https://fr.wikipedia.org/wiki/Comparaison_asymptotique
en faisant un développement limité:
or:
et
La série de terme général u_n est donc la somme d'une série alternée, convergente mais non absolument convergente, et d'une série absolument convergente.
Pour les notations "o" et "O" de Landau , voir ci-dessous:
https://fr.wikipedia.org/wiki/Comparaison_asymptotique
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
