Soient n , a et b des nombres entiers naturels non nuls tels que a>b et n²+1=ab
1) Montrer que a;)b;);)(4n;)3)
2) Trouver toutes les valeurs de n pour que l'égalité ait lieu
Inégalité olymp
4 messages
- Page 1 sur 1
Si on note 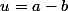 , la condition s'écrit
, la condition s'écrit =(n^2+1)) et donc b est racine de X^2+uX-(n^2+1).
et donc b est racine de X^2+uX-(n^2+1).
Le discriminant D est égal à .
.
Mais ce discriminant doit être un carré parfait (si on regarde les solutions, |2b+u| est un entier et est égal à la racine de D).
Or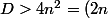^2) donc
donc ^2) et donc
et donc 
Le cas d'égalité est assez simple, il faut regarder les conditions pour que 4n-3 soit un carré parfait et que -rac(4n-3)+(2n+1) soit pair.
Le discriminant D est égal à
Mais ce discriminant doit être un carré parfait (si on regarde les solutions, |2b+u| est un entier et est égal à la racine de D).
Or
Le cas d'égalité est assez simple, il faut regarder les conditions pour que 4n-3 soit un carré parfait et que -rac(4n-3)+(2n+1) soit pair.
Salut,
1) On a évidement .
.
^2+1=a^2-2an+n^2+1=a(a-2n+b)\geq a\) donc
donc ^2=(a-n)^2-a+n+\frac{1}{4}\geq n-\frac{3}{4})
^2+1=b^2-2bn+n^2+1=b(b-2n+a)\geq b\) donc
donc ^2=(n-b)^2-b+n+\frac{1}{4}\geq n-\frac{3}{4})
d'où+\big(n-b+\frac{1}{2}\big)\geq\sqrt{n-\frac{3}{4}}+\sqrt{n-\frac{3}{4}}=\sqrt{4n-3})
2) Vu la preuve ci dessus, il y a égalité ssi soit
soit  et il faut que
et il faut que ^2+1\) soit (calculs)
soit (calculs) ^2+5=2(a+b)) .
.
On peut paramétrer les solutions en posant (par exemple) ,
,  d'où
d'où 
ce qui donne ,
,  et
et 
EDIT : pas assez rapide... :dodo:
1) On a évidement
d'où
2) Vu la preuve ci dessus, il y a égalité ssi
On peut paramétrer les solutions en posant (par exemple)
ce qui donne
EDIT : pas assez rapide... :dodo:
Modifié en dernier par Ben314 le 09 Jan 2016, 09:26, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Matt_01 a écrit:Si on note, la condition s'écrit
et donc b est racine de X^2+uX-(n^2+1).
Le discriminant D est égal à.
Mais ce discriminant doit être un carré parfait (si on regarde les solutions, |2b+u| est un entier et est égal à la racine de D).
Ordonc
et donc
Le cas d'égalité est assez simple, il faut regarder les conditions pour que 4n-3 soit un carré parfait et que -rac(4n-3)+(2n+1) soit pair.
j'ai pas compris apres
b²+bu-(n^2+1)=0
les solutions<100:
b= 1a= 2 n= 1
b= 1a= 5 n= 2
b= 1a= 10 n= 3
b= 1a= 17 n= 4
b= 1a= 26 n= 5
b= 1a= 37 n= 6
b= 1a= 50 n= 7
b= 1a= 65 n= 8
b= 1a= 82 n= 9
b= 2a= 5 n= 3
b= 2a= 13 n= 5
b= 2a= 25 n= 7
b= 2a= 41 n= 9
b= 2a= 61 n= 11
b= 2a= 85 n= 13
b= 5a= 10 n= 7
b= 5a= 13 n= 8
b= 5a= 29 n= 12
b= 5a= 34 n= 13
b= 5a= 58 n= 17
b= 5a= 65 n= 18
b= 5a= 97 n= 22
b= 10a= 17 n= 13
b= 10a= 29 n= 17
b= 10a= 53 n= 23
b= 10a= 73 n= 27
b= 13a= 25 n= 18
b= 13a= 34 n= 21
b= 13a= 74 n= 31
b= 13a= 89 n= 34
b= 17a= 26 n= 21
b= 17a= 53 n= 30
b= 17a= 85 n= 38
b= 25a= 41 n= 32
b= 25a= 74 n= 43
b= 26a= 37 n= 31
b= 26a= 85 n= 47
b= 29a= 58 n= 41
b= 29a= 73 n= 46
b= 34a= 65 n= 47
b= 34a= 89 n= 55
b= 37a= 50 n= 43
b= 41a= 61 n= 50
b= 50a= 65 n= 57
b= 58a= 97 n= 75
b= 61a= 85 n= 72
b= 65a= 82 n= 73
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
