Fonction périodique
94 messages
- Page 1 sur 5 - 1, 2, 3, 4, 5
Fonction périodique
Bonjour. Je rencontre quelques difficultés dans la résolution de cet exercice. Pouvez vous m'aider ? Voici l'énoncé: soit d un nombre irrationnel. Démontrer que la fonction f(x)=sin x + cos(dx) n'est pas périodique.
Merci !
Merci !
Sinon, on peut utiliser le résultat suivant :
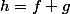 , continue sur
, continue sur  et non constante est périodique si et seulement si
et non constante est périodique si et seulement si  , avec
, avec 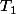 et
et 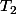 les périodes respectives de
les périodes respectives de  et
et  .
.
Dans notre cas,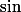 est
est  périodique et
périodique et 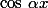 est
est  périodique. Or le rapport vaut
périodique. Or le rapport vaut  , irrationnel par hypothèse. Donc la fonction considérée n'est pas périodique.
, irrationnel par hypothèse. Donc la fonction considérée n'est pas périodique.
Dans notre cas,
Salut,
A mon avis, le plus simple est plutôt d'utiliser l'indic de ffpower qui demande uniquement comme connaissance de savoir que :
1) Si f est périodique de période T alors f" aussi
2) Si f et g sont périodiques de même période T alors, pour tout a,b dans R, a.f+b.g est aussi périodique de période T.
A mon avis, le plus simple est plutôt d'utiliser l'indic de ffpower qui demande uniquement comme connaissance de savoir que :
1) Si f est périodique de période T alors f" aussi
2) Si f et g sont périodiques de même période T alors, pour tout a,b dans R, a.f+b.g est aussi périodique de période T.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
La période T, si elle existe, d'une fonction f(x) somme de 2 fonctions périodiques g(x) de période T1 et h(x) de période T2, est T = a.T1 = b.T2 avec a et b dans N* tels que a/b est une fraction rationnelle irréductible.
a.T1 = b.T2
T2/T1 = a/b
*******
Dans le cas présent :
g(x) = sin(x), T1 = 2Pi
h(x) = cos(dx), T2 = 2Pi/d
T2/T1 = 1/d
1/d n'est pas rationnel et donc f(x) n'est pas périodique.
:zen:
a.T1 = b.T2
T2/T1 = a/b
*******
Dans le cas présent :
g(x) = sin(x), T1 = 2Pi
h(x) = cos(dx), T2 = 2Pi/d
T2/T1 = 1/d
1/d n'est pas rationnel et donc f(x) n'est pas périodique.
:zen:
Black Jack a écrit:La période T, si elle existe, d'une fonction f(x) somme de 2 fonctions périodiques g(x) de période T1 et h(x) de période T2, est T = a.T1 = b.T2 avec a et b dans N* tels que a/b est une fraction rationnelle irréductible.
a.T1 = b.T2
T2/T1 = a/b
*******
Dans le cas présent :
g(x) = sin(x), T1 = 2Pi
h(x) = cos(dx), T2 = 2Pi/d
T2/T1 = 1/d
1/d n'est pas rationnel et donc f(x) n'est pas périodique.
:zen:
Merci beaucoup ! C'est beaucoup plus clair
toutefois :
Ceci se justifie ?La période T, si elle existe, d'une fonction f(x) somme de 2 fonctions périodiques g(x) de période T1 et h(x) de période T2, est T = a.T1 = b.T2 avec a et b dans N* tels que a/b est une fraction rationnelle irréductible.
Salut,
ce genre d'exercice n'est pas facile, en tout cas surement pas de niveau seconde.
Ceci est malheureusement faux, il suffit de prendre h=-g pour s'en rendre compte.
Je pense que la preuve la plus "élémentaire" est celle proposée par ffpower, le problème est qu'elle ne s'adapte pas à toutes les situations. Dans un cadre plus général, pour étudier les périodes de f+g, il faut connaitre le résultat classique sur les sous-groupes additifs de R.
ce genre d'exercice n'est pas facile, en tout cas surement pas de niveau seconde.
La période T, si elle existe, d'une fonction f(x) somme de 2 fonctions périodiques g(x) de période T1 et h(x) de période T2, est T = a.T1 = b.T2 avec a et b dans N* tels que a/b est une fraction rationnelle irréductible.
Ceci est malheureusement faux, il suffit de prendre h=-g pour s'en rendre compte.
Je pense que la preuve la plus "élémentaire" est celle proposée par ffpower, le problème est qu'elle ne s'adapte pas à toutes les situations. Dans un cadre plus général, pour étudier les périodes de f+g, il faut connaitre le résultat classique sur les sous-groupes additifs de R.
Soit G un groupe abélien fini.
* Il existe une unique suite (a1,a2,...,ak) d'entiers > 1 telle que G soit isomorphe au produit direct des groupes cycliques de cardinal les différents éléments de la suite:
G\simeq \mathbb{Z}/a_1\mathbb{Z}\times \mathbb{Z}/a_2\mathbb{Z} \times \cdots \times \mathbb{Z}/a_k\mathbb{Z}\;,
et que ai+1 divise ai pour tout i entier entre 1 et k - 1.
* Les éléments de cette suite sont appelés facteurs invariants de G.
* Il existe une unique suite (a1,a2,...,ak) d'entiers > 1 telle que G soit isomorphe au produit direct des groupes cycliques de cardinal les différents éléments de la suite:
G\simeq \mathbb{Z}/a_1\mathbb{Z}\times \mathbb{Z}/a_2\mathbb{Z} \times \cdots \times \mathbb{Z}/a_k\mathbb{Z}\;,
et que ai+1 divise ai pour tout i entier entre 1 et k - 1.
* Les éléments de cette suite sont appelés facteurs invariants de G.
94 messages
- Page 1 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
