Comment démontrer qu'une fonction est périodique ? ( Modifié ! )
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nice
- Membre Relatif
- Messages: 291
- Enregistré le: 26 Jan 2009, 06:35
-
par nice » 13 Oct 2009, 20:29
psp a écrit:Je sais que j'en demande beaucoup, mais pourrais tu me faire la démonstration étape par étape s'il te plaît ? Je sais que pour toi ces calculs sont très simples, mais pour moi, c'est vraiment un gouffre !
Je t'en supplie !
bon ok
= 2sinx + cos2x)
= f(x+2\Pi) = 2 sin(x+2\Pi) + cos 2(x+2\Pi)= 2 sin (x+2\Pi) + cos(2x+4\Pi)
)
en utilisant les formules que je t'ai donné on a
*
 = 2 (sin x \times cos 2\Pi + cos x\times sin 2\Pi) = 2(sinx cos2\Pi + cos x sin 2 \Pi))
dans le cercle trigonometrique,
=
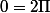
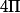
donc
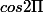
= cos 0 = 1 et
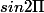
= sin0 = 0 d'où
= 2(sinx \times 1 +cos x\times 0)=)
2 sinx*
 = cos 2x cos 4\Pi - sin 2x sin 4\Pi= cos2x \times cos0 - sin2x\times sin0 = cos 2x \times 1-sin2x\times 0 =)
cos 2x en additionnant les resultats en couleur on a donc
f(x+
)=
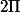
2sinx + cos2x
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
