Produit infini
Olympiades mathématiques, énigmes et défis
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Nov 2010, 18:22
par Nightmare » 12 Nov 2010, 18:22
Hello,
vu à l'instant sur un autre forum :
Calculer

.
:happy3:
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 12 Nov 2010, 18:36
par Euler07 » 12 Nov 2010, 18:36
C'est un super produit... Je m'y mets
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 12 Nov 2010, 19:23
par nee-san » 12 Nov 2010, 19:23
un bon produit, de quoi s'amuser
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 12 Nov 2010, 20:50
par nee-san » 12 Nov 2010, 20:50
mais en faite je viens de comprendre en quoi onsiste le produit mais tu attend quoi comme genre de reponse

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Nov 2010, 20:52
par Ben314 » 12 Nov 2010, 20:52
Un truc du style
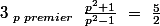
...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 12 Nov 2010, 20:53
par nee-san » 12 Nov 2010, 20:53
ah daccord merci bien
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 12 Nov 2010, 21:02
par Doraki » 12 Nov 2010, 21:02
c'est très joli
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Nov 2010, 21:17
par Nightmare » 12 Nov 2010, 21:17
Encore une bonne réponse d'oncle Ben ! Une preuve en une ligne avec la fonction zeta. Sans elle, pas sûr qu'on puisse élémentairement arriver au résultat.
-
nee-san
- Membre Irrationnel
- Messages: 1220
- Enregistré le: 04 Sep 2010, 20:23
-
 par nee-san » 12 Nov 2010, 21:26
par nee-san » 12 Nov 2010, 21:26
j'approchée du résultat mais comment vous êtes arriver a

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Nov 2010, 21:35
par Nightmare » 12 Nov 2010, 21:35
Cf mon message ci-dessus, on peut utiliser la fonction zeta de Riemann.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 12 Nov 2010, 23:12
par benekire2 » 12 Nov 2010, 23:12
Salut, ça me fait penser à l'identité :
=\Bigprod_{p}\frac{p^s}{p^s-1})
bon évidemment ça peut pas se "torcher" uniquement avec ça , je regarderais ça demain .
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 12 Nov 2010, 23:14
par Nightmare » 12 Nov 2010, 23:14
eh bien si, ça se "torche" en une ligne avec cette identitée :lol3:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 12 Nov 2010, 23:23
par benekire2 » 12 Nov 2010, 23:23
On va prendre s=2 puis on va réfléchir pour trouver la fin de cette ligne :ptdr: faut dire que zeta 2 c'est pi²/6 et que donc on veut 5/2 .. et il nous reste un "bout" les produits des (p²+1)/(p²) et ... je crois connaître ça ... :zen:
EDIT. En fait j'ai pas l'impression de connaître ce "bout" ...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Nov 2010, 00:43
par Ben314 » 13 Nov 2010, 00:43
Une grosse indic :
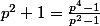
...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Nov 2010, 12:20
par benekire2 » 13 Nov 2010, 12:20
Ben314 a écrit:Une grosse indic :
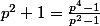
...
Je viens de regarder "en détail" le problème et j'avance pas par rapport à hier. J'ai le produit des p²/(p²-1) qui vaut zeta(2). Maintenant tu me donne cette "indic" alors il me reste plus qu'à calculer le produit des (p^4+1)/(p^4-p²) et donc j'en conclus qu'il ne fallait pas "sortir" le zeta(2) au début ...
Mais je réfléchis encore un peu ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Nov 2010, 12:39
par benekire2 » 13 Nov 2010, 12:39
benekire2 a écrit:et il nous reste un "bout" les produits des (p²+1)/(p²) et
Tout compte fait je m'en souviens .. enfin, je l'ai retrouvé ...
P l'ensemble des nombres premiers.
}{\zeta{4}}=\Bigprod_{p \in P}\frac{p^2}{p^2-1} . \frac{p^4-1}{p^4}=\Bigprod_{p \in P} 1+\frac{1}{p^2})
Et voilà ... :zen:
PS. Personne n'aurait un pdf sur les propriétés du genre (zeta(p)/zeta(2p)=..) sur la fonction zeta ? Qui , même si il s'embarque sur de l'analyse complexe "donne" les résultats ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Nov 2010, 13:09
par Ben314 » 13 Nov 2010, 13:09
benekire2 a écrit:PS. Personne n'aurait un pdf sur les propriétés du genre (zeta(p)/zeta(2p)=..) sur la fonction zeta ? Qui , même si il s'embarque sur de l'analyse complexe "donne" les résultats ?
Tsst, Tsst, Tsst : "regarder" des résultats dont on a pas vraiment l'utilité et dont on ne comprend pas la preuve = mauvaise démarche...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Nov 2010, 13:17
par benekire2 » 13 Nov 2010, 13:17
Ben314 a écrit:Tsst, Tsst, Tsst : "regarder" des résultats dont on a pas vraiment l'utilité et dont on ne comprend pas la preuve = mauvaise démarche...
Je voulais simplement voir quel genre de résultats on peut avoir en arithmétique avec la fonction zeta .. mais si tu dis que je dois pas , je fais pas :lol3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Nov 2010, 13:24
par Ben314 » 13 Nov 2010, 13:24
benekire2 a écrit:Je voulais simplement voir quel genre de résultats on peut avoir en arithmétique avec la fonction zeta .. mais si tu dis que je dois pas , je fais pas :lol3:
Je dit pas vraiment que tu "doit pas", mais plutôt qu'il ne faut pas prendre l'habitude de fonctionner comme ça (= petit singe savant).
Bon, aprés, il y a aussi (surtout ?) le fait que je sais pas quoi te donner comme "référence" :ptdr:
Le "Nombres premiers" de William John Ellison (en collaboration avec Michel Mendès France) chez Hermann doit surement contenir des trucs à ce propos, mais c'est un gros bouquin qui risque d'être "un peu chaud" à ton niveau..
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 13 Nov 2010, 13:30
par benekire2 » 13 Nov 2010, 13:30
Oui je comprends parfaitement ce que tu veut dire (= faut pas jouer au touche a tout ) , de manière générale je reste dans mon bouquin et je travaille les preuves. Ici on va dire que c'était l'exo qui m'avait alléché, mais après une rapide recherche sur internet il s'avère qu'on plonge dans l'analyse complexe et d'autres choses dont j'ignore tout de tout.
Pour le bouquin "les nombres premiers" , je doute fort que ce soit de l'arithmétique élémentaire , et comme c'est pas de mon niveau, ça servirait à rien .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
...