Un produit infini
9 messages
- Page 1 sur 1
par Doraki » 23 Sep 2010, 17:17
Ca ressemble vachement à ce qu'on trouve quand on approxime pi en regardant des polygones réguliers à 2^n cotés
par most » 04 Oct 2010, 08:14
salut :
par recurrence on a:
=({\sqrt { 2 + \sqrt { 2+ ...+\sqrt { 2}}}} )/2)
on pose:
A= cos (\pi /8)...cos(\pi /2^n))
en multipliant les deux membres par)
et en utilisant la formule:
on aura:
 A= sin (\pi /2)=1)
l'expression cherché c'est la limite de
quand n tends vers 
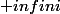
soit /( {\pi /2^n})) =\pi)
par recurrence on a:
on pose:
A=
en multipliant les deux membres par
on aura:
l'expression cherché c'est la limite de
soit
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :