Inegalite..
Olympiades mathématiques, énigmes et défis
-
Anonyme
 par Anonyme » 24 Déc 2009, 11:29
par Anonyme » 24 Déc 2009, 11:29
Bonjour
Je bloque sur une petite inégalité d'olympiade.
Soit
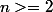
un entier , et

des reel tel que

Monter que

J'arrive pas a faire apparaitre

des l'inegalite.
Cet exo est pris du polycopie d'animath et normalement je dois utiliser que C-S, l'inegalite triangulaire et les inegalites avec des carres.
Merci
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 24 Déc 2009, 19:50
par kasmath » 24 Déc 2009, 19:50
pour tout

on a
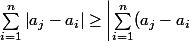\right| = \left|na_j - \sum^n_{i = 1}a_i\right| = n\left|a_j\right|\ \Rightarrow\ \sum^n_{i,j = 1}\left|a_j - a_i\right| = 2\sum^{ }_{1\leq i < j\leq n}|a_j - a_i| \geq n\sum^n_{j = 1}\left|a_j\right|\right.)
c'est trés facile
-
Anonyme
 par Anonyme » 26 Déc 2009, 13:57
par Anonyme » 26 Déc 2009, 13:57
Personne ? :doh:
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 26 Déc 2009, 15:47
par nodgim » 26 Déc 2009, 15:47
Es tu sûr de l'énoncé ?
-
poiuytreza
- Membre Naturel
- Messages: 72
- Enregistré le: 22 Avr 2009, 13:40
-
 par poiuytreza » 26 Déc 2009, 19:04
par poiuytreza » 26 Déc 2009, 19:04
Tu peux t'en sortir en n'utilisant que l'inégalité triangulaire...
Sinon, l'inégalité à montrer peut se réécrire sous la forme :

qui est plus facile à utiliser
-
Anonyme
 par Anonyme » 26 Déc 2009, 19:11
par Anonyme » 26 Déc 2009, 19:11
poiuytreza a écrit:Tu peux t'en sortir en n'utilisant que l'inégalité triangulaire...
Sinon, l'inégalité à montrer peut se réécrire sous la forme :

qui est plus facile à utiliser
merci beaucoup d'avoir repondu... :zen:
Mais comment tu est passer a cette forme ? (c'est intuitif mais une justification est necessaire)
Meme avec cette forme j'arrive pas avoir l'inegalite triangulaire :briques: :help:
-
poiuytreza
- Membre Naturel
- Messages: 72
- Enregistré le: 22 Avr 2009, 13:40
-
 par poiuytreza » 26 Déc 2009, 19:15
par poiuytreza » 26 Déc 2009, 19:15
Il suffit de multiplier chaque membre par 2, je ne suis pas sûr qu'il soit indispensable de justifier plus.
Sinon, pour montrer que :

il suffirait de montrer que pour tout i :

-
Anonyme
 par Anonyme » 26 Déc 2009, 19:48
par Anonyme » 26 Déc 2009, 19:48
poiuytreza a écrit:Il suffit de multiplier chaque membre par 2, je ne suis pas sûr qu'il soit indispensable de justifier plus.
Sinon, pour montrer que :

Je croyais qu'on pouvait atteindre ce resultat par un calcul ou du moins d'une façon mathématique .
poiuytreza a écrit:il suffirait de montrer que pour tout i :

la aussi a t- on le droit de "simplifier" par

sans justifier ?
Sinon en effet quand on arrive a ce point le problème est presque résolu l'inégalité est facile a demontrer
Merci :zen:
-
Anonyme
 par Anonyme » 26 Déc 2009, 19:57
par Anonyme » 26 Déc 2009, 19:57
Au fait on utilise ou l'inégalité triangulaire ? je ne l'ai pas utilise pour la dernière inégalité ou du moins sans le savoir :hein:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2009, 20:00
par girdav » 26 Déc 2009, 20:00
Qmath a écrit:Je croyais qu'on pouvait atteindre ce resultat par un calcul ou du moins d'une façon mathématique .
la aussi a t- on le droit de "simplifier" par

sans justifier ?
Sinon en effet quand on arrive a ce point le problème est presque résolu l'inégalité est facile a demontrer
Merci :zen:
En fait ce n'est pas une simplification à proprement parler. L'idée consiste à dire qu'une condition suffisante pour qu'une somme soit plus grande qu'une autre (avec les mêmes indices de sommation) est que chacun des termes soit plus grand.
Là, il se trouve que c'est le cas.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 26 Déc 2009, 20:00
par Skullkid » 26 Déc 2009, 20:00
Une justification un peu plus poussée du passage de

En gros ça marche parce que

est inchangé si on permute i et j, et nul si i = j.
Pour ta deuxième question, attention, poiuytreza n'a pas "simplifié" par

! Il t'a juste exhibé une inégalité qui impliquait celle que tu cherchais à démontrer, et de forme plus simple.
-
Anonyme
 par Anonyme » 26 Déc 2009, 20:14
par Anonyme » 26 Déc 2009, 20:14
Merci Skullkid pour la demo.
Oui je sais que ce n'est pas une simplification c'est pour cette raison que je l'ai mis entre guillemet. Comme j'ai presque jamais travailler avec des sommation je ne savais pas quel terme employe.
Pas si facile l'exo si on en a jamais fait pareil ...
Merci pour tout :zen: :++:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 27 Déc 2009, 11:48
par benekire2 » 27 Déc 2009, 11:48
J'avais également beaucoup de problèmes sur les sommations, et le truc c'est de s'entraîner et de se familiariser avec, et de revenir parfois aux écritures a rallonge, de manière a "voir" certaines simplifications.
Tu peut trouver les règles de bases dans la signature de tim, après c'est a toi de te débrouiller pour le reste ...
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 27 Déc 2009, 21:07
par kasmath » 27 Déc 2009, 21:07
kasmath a écrit:pour tout

on a
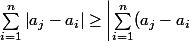\right| = \left|na_j - \sum^n_{i = 1}a_i\right| = n\left|a_j\right|\ \Rightarrow\ \sum^n_{i,j = 1}\left|a_j - a_i\right| = 2\sum^{ }_{1\leq i < j\leq n}|a_j - a_i| \geq n\sum^n_{j = 1}\left|a_j\right|\right.)
c'est une bonne idée si je me trompe pas
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
sans justifier ?