Inégalité

par **MMu** » 29 Mai 2024, 14:05

Soient les entiers

et les réels positifs

tels que

.
Notons

. Montrer que

par **MMu** » 31 Mai 2024, 16:21

Mea culpa, j’ai oublié d’indiquer que l’addition sur les indices est modulo

par **Ben314** » 31 Mai 2024, 21:13

En ce qui me concerne, j'avais compris, sauf que je suis bien sec sur ce coup là . . .

par **MMu** » 15 Juil 2024, 16:16

C’est un peu fastidieux mais pas bien compliqué.
On note

...donc...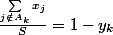

On peut donc écrire

La fonction

avec

est convexe (je vous laisse vérifier :frime:

) et donc avec Jensen on peut écrire

avec

Comme d’autre part

on obtient finalement

.. q,e,d

par **MMu** » 15 Juil 2024, 23:30

Je corrige une erreur de frappe :