des nombres réels positifs. Prouver que
Inégalité
8 messages
- Page 1 sur 1
Re: Inégalité
Salut,
J'ai une soluce, mais à peine bourinne.... :

En considérant que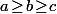 donc que
donc que 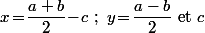 sont positifs.
sont positifs.
(ça prouve aussi qu'il y a égalité ssi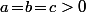 ou bien
ou bien 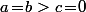 )
)
J'ai une soluce, mais à peine bourinne.... :

En considérant que
(ça prouve aussi qu'il y a égalité ssi
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Inégalité
Tout simplement parce que "la fin justifie les moyens", c'est à dire qu'en remplaçant a,b,c par ça, il s'avère que le résultat qu'on obtient est clairement positif (somme de nombres positifs) donc ça prouve effectivement le truc demandé (et ça permet même de voir quels sont exactement les cas d'égalité).scardy123 a écrit:Merci, mais pourquoi remplacez-vousavec
et
avec
?
Par contre, le POURQUOI avec cette substitution là, on obtient un résultat trivialement positif, ben ça j'en sais rien...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Inégalité
Bonjour
Voici une autre solution que je propose.
Je pose S=" membre de gauche - membre de droite" et je réduit au même dénominateur pour trouver que S est positif ssi le numérateur est positif
i.e=a^5 - a^3 b^2 - a^2 b^3 + b^5 + a^2 b^2 c - a^3 c^2 + a^2 b c^2 + a b^2 c^2 - b^3 c^2 - a^2 c^3 - b^2 c^3 + c^5\geq 0 ?) on a aussi
on a aussi
h(-a,-b,-c)=-h(a,b,c)
Donc je suppose que a,b et c sont négatifs et il faut donc montrer que\leq 0.)
Je pose; s_2= a^2+b^2+c^2; s3=-abc)
et grâce aux symétries, un calcul donne
=-s1^5 + 5 s1^3 s2 - 4 s1 s2^2 - 7 s1^2 s3 + 3 s2 s3)
Le polynôme (d'Hurwitz)=x^3+s1x^2+s2x+s3) ayant ses 3 racines a,b,c strictement négaitves
ayant ses 3 racines a,b,c strictement négaitves
alors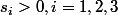 et
et 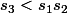
Je majore donc h(a,b,c) en remplaçant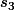 par
par 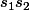
On a alors\leq -s1^5 - 2 s1^3 s2 - s1 s2^2=-s1 (s1^2 + s2)^2\leq 0)
Je n'ai pas le temps de regarder les détails mais ça doit être bon.
Voici une autre solution que je propose.
Je pose S=" membre de gauche - membre de droite" et je réduit au même dénominateur pour trouver que S est positif ssi le numérateur est positif
i.e
h(-a,-b,-c)=-h(a,b,c)
Donc je suppose que a,b et c sont négatifs et il faut donc montrer que
Je pose
et grâce aux symétries, un calcul donne
Le polynôme (d'Hurwitz)
alors
Je majore donc h(a,b,c) en remplaçant
On a alors
Je n'ai pas le temps de regarder les détails mais ça doit être bon.
Re: Inégalité
Ben ça, c'est écrit en noir sur blanc dans le post : si tu prend des réels quelconques a,b,c tels quescardy123 a écrit:Ok, mais je n'ai pas compris pourquoi il est légitime que le remplacement ...
Et ça prouve que ça démontre bien le résultat dans toute ça généralité.
@aviateur : c'est (bien évidement) en jouant avec les polynômes symétriques et les liens avec les racines (et Mapple...) que j'ai fini par tomber sur la substitution "magique" ci dessus.
Sauf que perso., vu l'homogénéité de la formule, j'avais pris dès le départ a+b+c=1 (c'est à dire s1=1 ce qui donne du degré bien plus petit dans le truc à étudier), puis, n'arrivant à rien de bien élémentaire, j'ai finalement j'ai pris c=1 pour n'avoir que 2 variables (et ça explique le changement de variable clairement non symétrique en c).
Modifié en dernier par Ben314 le 21 Déc 2017, 15:20, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

