Soit
Montrer qu'il existe
Bonne chance.
Thomas G :zen:
Dérivée et inégalité
4 messages
- Page 1 sur 1
dérivée et inégalité
par nekros » 21 Juil 2006, 18:30
Bonsoir,
Soit
de 
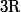
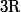
dans de classe 
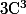
dans .
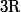
Montrer qu'il existe
tel que :
f'(a)f^{2}(a)f^{3}(a) \ge 0})
où 
est la dérivée nième de .
Bonne chance.
Thomas G :zen:
Soit
Montrer qu'il existe
Bonne chance.
Thomas G :zen:
par girdav » 19 Aoû 2009, 13:39
En fait si 
s'annule c'est évident.
Si elle ne s'annule pas, comme elle est continue, elle est soit toujours positive soit toujours négative (strictement). On peut supposer positive, sinon on pose 
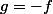
et g'(x)g''\(x\)g^3(x) = (-1)^4f(x)f'(x)f''\(x\)f^3(x)= f(x)f'(x)f ''\(x\)f^3(x))
.
Donc tout se ramène à chercher
tel que f''\(a\)f^3\(a\) \geq 0)
.
On suppose que
ne s'annule pas. Mais cette fois il faut distinguer le cas 
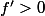
et 
.
Si elle ne s'annule pas, comme elle est continue, elle est soit toujours positive soit toujours négative (strictement). On peut supposer
Donc tout se ramène à chercher
On suppose que
par girdav » 19 Aoû 2009, 20:17
Timothé Lefebvre a écrit:Wahou voila un champion du deterrage de post !
Heureusement que les maths viellissent bien!
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :