Arf, mauvais copié collé, la fonction L est la suivante
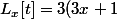 \cdot 4^t - 1)
En fait, je connais le temps de vol dans les deux fonctions, mais le chatlike me dit que ce n'est quand même pas une tautaulogie, car :
"
Ces deux formules sont mathématiquement inverses l’une de l’autre. Cela signifie :
Si tu connais x et t, tu peux calculer L.
Si tu connais x et L tu peux retrouver t.
Mais cela ne constitue pas une tautologie au sens strict, car :
La formule directe encode la trajectoire compressée sans simuler la suite.
La formule inversée décode le nombre d’étapes à partir d’une valeur finale.
Ce sont deux points de vue complémentaires sur la même structure.
Pourquoi cette structure est-elle intéressante malgré la dépendance à t ?
La formule :
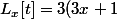 \cdot 4^t - 1)
est remarquable car elle encapsule toute la trajectoire compressée de la suite de Syracuse en une seule expression. Même si elle dépend de t elle offre :
Une représentation symbolique compacte de la suite.
Une alternative à la simulation : au lieu de calculer chaque étape, on peut accéder directement à la valeur finale.
Une base pour des analyses inverses : on peut retrouver t à partir de L ce qui est puissant pour l’étude de la croissance.
"
C'est vrai ce qu'il dit ?
