10 étapes pour un seul chiffre

[Imod]

Bonsoir à tous :zen:

J'ai ajouté un indice sur les maths.net , je n'ai pas le courage de le recopier ici mais je voulais quand même vous en informer .

Bon courage et bon amusement à tous .

Imod

[nodjim]

Imod, tu maintiens qu'au terme d'une seule étape on arrive à un nombre <= 1000 ? Même avec une suite de 1001 chiffres 1 ?
Je vois pas trop comment tu pourrais faire....

[Ben314]

Je pense que j'ai la solution :
Si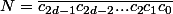 (écriture décimale avec éventuellement 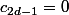) on pose 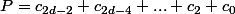et .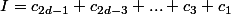

Alors, la somme des chiffres de N pris "un par un" est clairement .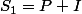

D'un autre coté, la somme des chiffres "pris 2 par 2" peut être égale à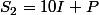 ou bien à selon la façon dont on forme les paires.

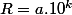Si on prend le plus grand des 2 il est nettement plus grand que S (j'ai la flemme de rentrer dans les détails de calcul...) et il y a suffisement de marge pour qu'il existe entre et un entier "rond" où a est un simple chiffre.
Or on peut "passer" de à à regroupant les uns aprés les autres les couples de chiffre.
Comme le passage de c+c' à 10c+c' se fait en augmentant de 9c, c'est à dire au max de 9.9=81, à force de regrouper les chiffres 2 par 2, on va tomber sur un nombre qui dépasse R de moins de 80 et donc dont la somme des chiffres est, au max a+8+9 c'est à dire au max une vingtaine (et le tout en uniquement 2 étapes)

[Ben314]

Exemple avec 123 456 789 fois le chiffre 1 :
S1=1+1+...+1 (123 456 789 fois) = 123 456 789
S2=11 +11 +11 +...+ 11 (61 728 394 fois) + 1 = 679 012 335
nombre "rond" entre les deux R=200 000 000 (par exemple)
en prenant k fois le couple 11 et 123 456 789 - 2k fois le chiffre 1, la somme obtenue est
S=11k + (123 456 789 - 2k) = 123 456 789 + 9k qui dépasse R pour k=8 504 802 et qui donne
S=200 000 007 dont la somme des chiffres est 9

[Imod]

Ca à l'air de coller Ben c'est pour ça que je disais que 4 étapes étaient sans doute trop . Il y a une façon simple de justifier le résultat en 4 étapes en faisant des regroupement en 4 chiffres au lieu de 2 .

Imod

[Ben314]

Pour rentrer dans les "détails" de calculs, on peut écrire que :
1) Si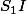 alors 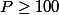et on prend
Donc on a forcément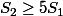 ce qui prouve qu'entre et il y a un nombre "rond" de la forme 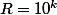ou bien de la forme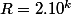

Vu que lorsque l'on regroupe les chiffres 2 par 2, ça fait augmenter la somme d'au max 81, on peut trouver une somme S comprise au sens large entre R et R+80 donc dont la somme des chiffres est, au max, 2+7+9=18 et on termine au pire avec une étapes de plus (soit 3 étapes au max)


Conclusion : sauf erreur, en 3 étapes au max, c'est plié.

[nodjim]

Je crois que j'ai.
On évalue la taille du nombre en additionnant tous les chiffres. On part de cette taille là (n chiffres) pour construire un nombre qui commence par 9. Pour ça, on prend les chiffres à la suite les uns des autres (G à D) jusqu'à n chiffres, puis on prend les chiffres suivants de n ou n-1 chiffres, selon le 1er chiffre du nombre formé, jusqu'à obtenir un 9 en 1er chiffre du nombre résultat. Ensuite on recommence l'opération et on cherche à obtenir un 9 en 2ème chiffre du nombre résultat. Et ainsi de suite.
Il faut comprendre qu'il n'y a aucune comparaison entre le nombre obtenu et le nombre de chiffres initiaux, c'est à dire que le nombre de chiffres qu'on a à notre disposition pour former le nombre résultat est quasiment illimité. Enfin, on terminera en faisant un plus que 9, de sorte qu'il ne restera que le nombre 1000......et des poussières.

[Imod]

Faut que je vérifie dans le détail Ben mais si ça marche ( ce que j'ai tendance à croire ) tu arriverais à 1 seul chiffre en un maximum de 3 étapes ce qui est mieux que les 4 étapes qu'on peut atteindre en formant des nombres de 3 ou 4 chiffres .

Imod