Le "zéro complexe" vs le "zéro réel" (Oui, je parle de math

[Bastien L.]

Bonjour!


Ma question n'a probablement pas d'utilité pratique pour le bac, mais bon…

On nous a dit que le nombre zéro complexe, quoiqu'il soit écrit "0", n'est pas le zéro réel…

Pourtant, sachant que la droite des réels faît partie de l'ensemble des complexes, son zéro est au moins un zéro des complexes, non?

Pourraît-il en exister d'autre?

Si (où 0 désigne dans les deux cas notre zéro réel) est juste (peut-être me direz-vous que non?), alors, on peut démontrer facilement que , c'est-à-dire que le zéro complexe est le zéro réel, non?


Voilà, merci d'avance…

[Huppasacee]

Bonjour

il est vrai que pour les calculs , le zéro des complexes est assimilable au zéro des réels
mais aussi , il pourrait être assimilé au zéro des imaginaires purs !

cela pour dire que en fait le zéro complexe peut s'écrire ( 0 ; 0), ce n'est pas uniquement 0
aussi , quand on étudie le corps des complexes , on fait la distinction

et, dans les calculs, on ne peut que les assimiler et non dire qu'ils sont égaux

[Bastien L.]

Bonjour

il est vrai que pour les calculs , le zéro des complexes est assimilable au zéro des réels
mais aussi , il pourrait être assimilé au zéro des imaginaires purs !

Bonjour à vous, merci pour la réponse rapide. :happy2:

En effet, mais j'avais justement la notion (peut-être éronnée…) que 0 était le point d'intersection entre la droite des réels et celle des imaginaires purs… Et que donc il était l'un et l'autre en même temps, le seul nombre à la fois réel et imaginaire pur…

(Je me demande alors accessoirement si dans ces conditions on peut vraiment dire qu'il est un réel, mais bon…)

J'ai entendu dire que certains considèrent les réels comme les nombres à 1 D, les complexes, comme les nombres à 2 D, les vecteurs, comme les nombres à 3D. Je ne sais si ç'a un sens et si c'est juste…

Mais j'en ai aussi connus certains qui écrivaient "0" sans flèche comme résultat de la somme de deux vercteurs opposés, volontairement, prétextant "Mais quelle est la nature de 0? Est-ce un nombre ou un vecteur?".

Si l'histoire des dimensions est juste, alors, l'argument de ceux qui écrivent "0" au lieu du vecteur nul devrait pouvoir se reporter pour les complexes…

Pourquoi 0 n'aurait-il pas la particularité de rester toujours le même quelque-soit le "type" de nombres considéré?

[Huppasacee]

Ceux qui ne mettent pas de flèche sur le vecteur
font un erreur grave
un vecteur est un vecteur
que sa norme soit nulle ou non
donc , lorsqu'on fait des calculs dans un ensemble, on y reste

[Bastien L.]

:doh: Oulah, c'est formel et peremptoire, comme réponse…

[Huppasacee]

excuse moi si le ton t'a paru sec
ce n'était pas mon intention
c'était une simple remarque ! , pas plus

[Bastien L.]

Non, non, je ne veux pas dire que je me sois vexé! :happy2:

Mais je trouve que la question appelle quand-même à réfléchir… À moins que tu n'aies des arguments, mais tu n'en as pas donnés…

[Charles D.]

J'essaye de répondre comme je peux la question est intéressante.
Si les 0 ne sont pas les mêmes dans les réels et dans les complexes pouvons nous affirmer que l'ensemble réel est alors inclus dans l'ensemble complexe? Si oui il existe donc deux zéros dans les complexes et alors on peux se poser la question du résultat de l'addition ou de la soustraction de ces deux zéros.

[Florélianne]

Bonjour,
Si je peux intervenir dans le débat, je vous direz simplement que tout le monde a un peu raison et un peu tort...
En fait tout ce qu'on présente comme des égalités qui mènent à des inclusions sont seulement des homéomrphismes... (même forme)
ensuite on les considère comme égaux, mais ceci est vrai depuis Z, le 0 de Z est-il le même que celui de IN ? là aussi on a +0 et - 0 ? etc...
Pour C on a deux homéomorphismes le premier entre les nombres écrits sous la forme a +0i et IR, le second entre C est le plan affine...
voilà pourquoi on peut considérer ( 0; 1 ; i) comme une base ce qui tendrait à placer des flêches, mais une flêche sur 1 ?
Sur ce bonne continuation dans l'amour des math. et de son prochain !

[Huppasacee]

Pour ce qui est des complexes et des réels , la frontière est mince
d'ailleurs R est inclus dans C, et les réels sont des complexes à partie imaginaire nulle

Par contre, pour ce qui est des vecteurs , l'espace est un espace vectoriel à 3 dimensions
si on situe dans l'espace , il faut donner les 3 dimensions
si un vecteur a une coordonnée nulle , c'est dans une base bien particulière, il suffit de changer de base pour que ses 3 coordonnées soient non nulles ( si ce vecteur n'est pas le vecteur nul )
et l'application "somme " de 2 vecteurs est une application interne, et donnera donc un vecteur et non un nombre
l'espace est un R espace vectoriel à 3 dimensions
et il y a une application " norme " qui à un vecteur associe un réel ( un nombre

[Bastien L.]

Bonjour, merci pour votre réponse.


Il me faudra un peu de lecture pour la saisir vraiment, mais elle m'inquiète - elle me trouble - en ceci: si je comprends bien, ça voudrait dire que l'ensemble des entiers naturels n'est pas réellement exclu dans celui des entiers relatifs? Donc 3 n'est pas +3?

Je sens que ce débat doit pouvoir devenir intéressant… ^^

Merci, et à bientôt (quand je serai suffisemment renseigné pour pouvoir poursuivre…)!

[Charles D.]

Donc la différence entre deux 0 d'ensembles différents n'est pas au niveau de leur valeur, mais au niveau de leur nature? Ce qui voudrait dire (pardonnez-moi si je sort une énormité) que le nombre 0 ne peut exister indépendamment d'un ensemble auquel il se rapporte?
Pourtant un nombre reste un nombre :mur:

[Florélianne]

Re-bonjour,
Exact, un nombre reste un nombre, et pour un mathématicien habitué à jongler avec des équivalences c'est tout naturel, mais pour les profanes ou les débutants c'est plus dur à saisir... un peu comme les vecteurs (et leurs représentants !) c'est purement abstrait...
mais pour le comptable 0 pour lui c'est 0...
c'est comme pour la calculatrice : tant qu'elle nous donne le bon résultat, inutile de se poser des questions sur la façon dont on l'a faite !
Bref, si vous trouvez que ça vous dépasse, vous pouvez vous en passer et vous servir du 0 sans poser de question...
les problèmes métaphysiques n'intéressent pas la plupart des gens... alors pourquoi la nature de 0 pourrait-elle être plus importante que la votre !
Sur ceux, vivez en paix , avec les math. et vous-mêmes...

[Sve@r]

Donc la différence entre deux 0 d'ensembles différents n'est pas au niveau de leur valeur, mais au niveau de leur nature? Ce qui voudrait dire (pardonnez-moi si je sort une énormité) que le nombre 0 ne peut exister indépendamment d'un ensemble auquel il se rapporte?

C'est pour ça que la notion du zéro a été si difficile à émerger au milieux de nombres dont le but initial était de dénombrer ce qui est dénombrable. Et il y a eu le même problème avec la notion d'espace où chaque objet est décrit par un point ou un ensemble de points. Le concept d'espace a été précédé par celui, plus simple, d'emplacement d'un objet et l'idée d'espace est venue lorsqu'on s'est posé la question de savoir si "l'emplacement" existait indépendamment du fait qu'un objet y soit situé ou non.

Je sens que ce débat doit pouvoir devenir intéressant… ^^

Oui, c'est pour ça que je l'ai déplacé dans une partie du forum destiné aux discussions mathématiques

[Bastien L.]

Bonjour Sve@r,


Merci aux uns et aux autres. L'attention avec laquelle sont rédigées vos réponses est toujours sensible, et c'est toujours un plaisir que de philosopher sur ce forum! [Pour ceux qui seraient choqués par le verbe à l'infinitif, demandez-vous ce que sont les mathématiques…]

Bref, si vous trouvez que ça vous dépasse, vous pouvez vous en passer et vous servir du 0 sans poser de question...
les problèmes métaphysiques n'intéressent pas la plupart des gens... alors pourquoi la nature de 0 pourrait-elle être plus importante que la votre !
Sur ceux, vivez en paix , avec les math. et vous-mêmes...

Non! Quelle horreur! (d'arrêter de réfléchir parce-que ce n'est pas absolument nécessaire, j'entend…) ^^ Ainsi que je l'ai précisé dès le premier message de cette discussion, je sais que cela n'a probablement pas d'importance pour la copie de bac ou pour calculer une concentration en chimie… Notre but, à Charles et à moi-même, est de profiter de ce qu'un point du chapitre sur les nombres complexes nous laisse un tout petit peu entrevoir ce problème, pour nous rendre compte de ce qu'il y a des questions à se poser, et ainsi de suite…

Le raisonnement donné par Florélianne est très intéressant mais il me semble qu'il pose certains problèmes.

Laissons de côté les cas les plus difficiles, 0, et l'ensemble des complexes, pour le moment.

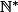
Mais prenons cet exemple: si je ne sais travailler que dans , et que je souhaite effectuer la division de 3 par 2, je me rends compte que je ne peux pas. Alors, je décide de découper chaque entier en un certain nombre fini de parts égales. Ici, je décide de découper les entiers en (au moins) deux parties égales, car je me rends compte que c'est suffisant pour pouvoir ensuite faire deux "tas" avec ces parties qui soient égaux l'un à l'autre. Et je décide, comme je compte déjà en base 10, pour pouvoir conserver la même écriture que d'habitude, que je découperai plutôt mes entiers en un nombre multiple de 10 de parts. Et j'écris le résulat de mon calcul ainsi: 1,5. 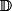J'ai créé (ce n'est pas internationnal, mais tant-pis).
Si j'ai écrit ces lignes, ce n'est pas pour faire du remplissage, mais pour arriver à ceci: 1,5 a été créé dans le but qu'on puisse diviser 3 par 2. C'est le nombre résultat de ce calcul. Ainsi, il semble qu'il est dans la nature de ce nombre que quand il sera multiplié par 2 il redonnera le 3 de d'où nous sommes partis! 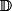Ce serait paradoxal si, en le multipliant par 2, nous disions trouver "le 3 de ", et ne pas pouvoir retrouver le 3 de !

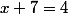
Or, historiquement, c'est bien un peu ainsi que les ensembles se sont formés… Alors, on peut renier toute cette histoire, dire que les hommes se sont trompés, que d'avoir créé n'a jamais permis de résoudre l'équation , 7, élément de parce-que, dès lors qu'on utilise x de , quoiqu'on lui fasse subir, il ne donnera jamais un élément d'un autre ensemble que celui auquel il appartient, il ne donnera au mieux qu'un élément de l'ensemble auquel il appartient ayant des propriétés proches de certains éléments de … Mais, franchement, dans l'état actuel des choses, je ne suis pas convaincu…

Voilà donc pourquoi l'application dans l'absolu du raisonnement de Florélianne me pose problème.

Ce qui ne signifie pas qu'il soit faux dans le cas qui nous préoccupe dans cette conversation.

Mais, s'il s'avère qu'il est faux dans certains cas et vrai dans d'autres, alors nous devrions être en mesure de déterminer qu'ont en commun les situations dans lesquelles il est vraie, et qu'ont en commun les situations dans lesquelles il est faux (ou, plutôt, "qu'est-ce qui fait que…"), et, ainsi, pouvoir revenir mieux armés à notre problème initial…

[Charles D.]

on peut renier toute cette histoire, dire que les hommes se sont trompés, que d'avoir créé n'a jamais permis de résoudre l'équation ,

C'est un détail mais tu voulais surement dire non?

[SimonB]

Bonjour,

Effectivement, c'est intéressant de se poser ce genre de questions.

Une petite remarque d'abord :

Mais prenons cet exemple: si je ne sais travailler que dans , et que je souhaite effectuer la division de 3 par 2, je me rends compte que je ne peux pas. Alors, je décide de découper chaque entier en un certain nombre fini de parts égales. Ici, je décide de découper les entiers en (au moins) deux parties égales, car je me rends compte que c'est suffisant pour pouvoir ensuite faire deux "tas" avec ces parties qui soient égaux l'un à l'autre. Et je décide, comme je compte déjà en base 10, pour pouvoir conserver la même écriture que d'habitude, que je découperai plutôt mes entiers en un nombre multiple de 10 de parts. Et j'écris le résulat de mon calcul ainsi: 1,5. J'ai créé (ce n'est pas internationnal, mais tant-pis).

Bon, en réalité, on crée plutôt comme ça. ça n'a pas été créé autrement que pour faire des calculs pratiques (avec nos maigres doigts). Et en maths, ça manque de propriétés intéressantes (le fait d'être un corps par exemple).

Et une deuxième :

Tu as raison sur la suite. Mais en général, dans ce genre de constructions (à partir d'un ensemble donné), il y a deux manières de voir l'ensemble qu'on a construit à la fin :

-comme un sur-ensemble de l'ensemble de départ dans lequel les choses se passent "mieux" (i.e. on peut faire les calculs comme on veut, par exemple "trouver un inverse pour 3 pour la multiplication" à partir de , ou "trouver un nombre dont le carré soit -1" à partir de ). C'est la vision "pragmatique" : celle qui doit prévaloir moralement quand on manipule l'ensemble.

-comme un ensemble construit certes à partir de l'ensemble de départ, qui n'est pas formellement parlant un sur-ensemble de celui de départ. Par exemple pour : formellement, dans la façon classique (la seule que je connais à vrai dire) de le construire, n'est pas vraiment inclus dans : on construit les fractions d'éléments de (où le dénominateur est non nul quand même...) à partir d'une relation d'équivalence ad hoc. Et après, on identifie à l'ensemble des nombres qui s'écrivent , où n est lui-même un entier relatif ! C'est la vision du bâtisseur "aveugle" de l'ensemble, celle qu'aurait une machine qui ne voit pas pourquoi on a construit ledit ensemble.

Là où les choses vont bien... C'est qu'en réalité, il y a des théorèmes d'identification, c'est-à-dire qu'on peut considérer l'ensemble de départ comme un sous-ensemble du machin construit : il y a ce qu'on appelle généralement un isomorphisme entre l'ensemble de départ ( dans mon exemple) et une partie de l'ensemble d'arrivée (l'ensemble des fractions dans mon exemple). C'est-à-dire que c'est finalement le même objet mathématique qu'on manipule.

Ce qui justifie le fait que dans la vie de tous les jours (la vie matheuse de tous les jours, s'entend...), on n'ait pas besoin de s'en préoccuper plus que ça. Mais c'est exact que ça demande une certaine réflexion pour s'en persuader.

NB : j'espère que le texte ne paraît pas trop difficile pré-bac, avec ces gros mots comme "corps" ou "isomorphisme". Ce sont des notions définies un peu plus tard, mais tu peux toujours consulter si ça t'intéresse Wikipédia par exemple pour voir ce que c'est...

[Charles D.]

Là où les choses vont bien... C'est qu'en réalité, il y a des théorèmes d'identification, c'est-à-dire qu'on peut considérer l'ensemble de départ comme un sous-ensemble du machin construit : il y a ce qu'on appelle généralement un isomorphisme entre l'ensemble de départ ( dans mon exemple) et une partie de l'ensemble d'arrivée (l'ensemble des fractions dans mon exemple). C'est-à-dire que c'est finalement le même objet mathématique qu'on manipule.

Voila tout le problème tourne autour de ce verbe ! On peut considérer le 0 réel et le 0 complexe sont les mêmes. Mais au fond qu'en est-il? je suis conscient que ça passe comme du chipotage, savoir que nous convenons que c'est le même objet mathématique suffit pour faire des mathématiques ,c'est commode, mais tu nous dit alors qu'ils sont extrêmement proches et donc qu'ils sont diffèrent.
Et c'est à ce moment-la que la question "en quoi sont-ils diffèrent?" arrive au galop. C'est ça qui est intéressant.

[SimonB]

Voila tout le problème tourne autour de ce verbe ! On peut considérer le 0 réel et le 0 complexe sont les mêmes. Mais au fond qu'en est-il? je suis conscient que ça passe comme du chipotage, savoir que nous convenons que c'est le même objet mathématique suffit pour faire des mathématiques ,c'est commode, mais tu nous dit alors qu'ils sont extrêmement proches et donc qu'ils sont diffèrent.
Et c'est à ce moment-la que la question "en quoi sont-ils diffèrent?" arrive au galop. C'est ça qui est intéressant.

Le verbe "pouvoir" signifie qu'on peut, dans les calculs, faire comme si c'était pareil. Comme je l'ai dit, c'est en soi différent en cela que le nouvel ensemble n'est pas construit formellement comme un sur-ensemble de l'ancien mais comme autre chose (un quotient par une relation d'équivalence, souvent).

Je ne dis pas qu'ils sont "extrêmement proches", je dis que leur comportement (vis-à-vis des lois que tu te donnes sur ton ensemble : addition, multiplication...) est exactement le même. C'est ça qui est important et qui fait que c'est pareil. Pour prendre un exemple simple, et pour plagier David Hilbert : si tu changes les noms des concepts "point, droite, plan" par les noms "verre de bière, chaise, table", tu ne changes pas les concepts. Tu as juste des théorèmes qui s'énoncent différemment ("l'intersection de deux chaises est ou bien vide, ou bien une chaise, ou bien un verre de bière", par exemple). De même, si tu dis que ce que nous désignons habituellement par le zéro des entiers naturels va dorénavant se désigner par "Marcel Proust", le un par "Zéro" et le deux par "La tête à toto", tu obtiens : Zéro+Zéro=La tête à toto.

Ce que j'écris est caricatural, mais c'est pour bien faire comprendre que non, il n'y a pas de différence de comportement entre les deux objets que tu construis, c'est-à-dire que même si les noms des objets sont différents, les relations entre eux sont les mêmes. Et c'est cela qui importe.

[Charles D.]

je me doute bien que le signifiant importe peu du moment qu'on comprend le signifié. Ce qui a choqué Bastien, c'est que ce matin-même nous apprenons que ces deux zéros ne sont pas rigoureusement les même mais la faute ne change rien. Ton explication me parait satisfaisante par contre tu a parlé de théorèmes d'identification, si tu possède une référence précise a ces théorèmes ils m'intéressent.