Question de sémantique
Question de sémantique
Bonsoir,
Il y a très longtemps que je n'ai pas fait de maths, alors, j'ai besoin d'une bonne remise à niveau [je sais on s'en était rendu compte :cry:]
Si j'écris "Soit la fonction f(x, y, z), telle que blablabla ..." est une faute de vocabulaire ?
Si oui, que devrais-je dire ?
Il y a très longtemps que je n'ai pas fait de maths, alors, j'ai besoin d'une bonne remise à niveau [je sais on s'en était rendu compte :cry:]
Si j'écris "Soit la fonction f(x, y, z), telle que blablabla ..." est une faute de vocabulaire ?
Si oui, que devrais-je dire ?
Salut, en toute rigueur c'est incorrect puisque f(x,y,z) c'est l'image de (x,y,z) par f, ce qui n'a aucune raison d'être une fonction, et encore moins la fonction f elle-même. Après, c'est un abus de langage qu'on fait souvent (en physique on le fait même tout le temps) lorsqu'il n'y a aucune ambiguïté. Comme tous les abus de langage, ça ne pose pas de problème de l'utiliser une fois qu'on a bien compris en quoi c'est un abus.
Des exemples de rédaction correctes sont "soit f(x,y,z) = ..." ou "soit f la fonction définie par f(x,y,z) = ...". Personnellement j'essaye au maximum d'utiliser les formulations correctes quand je poste sur le forum, sauf quand je sais que mon interlocuteur ne sera pas induit en erreur par les abus de langage.
Des exemples de rédaction correctes sont "soit f(x,y,z) = ..." ou "soit f la fonction définie par f(x,y,z) = ...". Personnellement j'essaye au maximum d'utiliser les formulations correctes quand je poste sur le forum, sauf quand je sais que mon interlocuteur ne sera pas induit en erreur par les abus de langage.
Bon je vais être plus précis, à partir d'un exemple.
J'ai une "relation" dans un espace 3D, qui se manifeste par une surface gauche. A certaines conditions (hors sujet), je peux écrire :
x=f(y, z) ; y=g(x, z) ; z =h(x, y)
il est bien évident que l'une de ces 3 fonctions (mot correct) implique les autres.
Donc, comment dois-je appelez f(x, y, z) ? Relation ?
J'ai une "relation" dans un espace 3D, qui se manifeste par une surface gauche. A certaines conditions (hors sujet), je peux écrire :
x=f(y, z) ; y=g(x, z) ; z =h(x, y)
il est bien évident que l'une de ces 3 fonctions (mot correct) implique les autres.
Donc, comment dois-je appelez f(x, y, z) ? Relation ?
Dlzlogic a écrit:Bon je vais être plus précis, à partir d'un exemple.
J'ai une "relation" dans un espace 3D, qui se manifeste par une surface gauche. A certaines conditions (hors sujet), je peux écrire :
x=f(y, z) ; y=g(x, z) ; z =h(x, y)
il est bien évident que l'une de ces 3 fonctions (mot correct) implique les autres.
Donc, comment dois-je appelez f(x, y, z) ? Relation ?
Ben je sais pas puisque tu dis pas ce qu'est f(x,y,z). Si c'est un nombre tu appelles ça un nombre, si c'est une fonction tu appelles ça une fonction, si c'est une relation tu appelles ça une relation, et si c'est une framboise tu appelles ça une framboise.
Tu dis que ton problème de départ c'est une relation sur un espace 3D. Donc à chaque point de l'espace tu peux associer un ou plusieurs points de l'espace, ce qui peut éventuellement s'interpréter comme une fonction de R^3 dans P(R^3). Après tu parles de f, g et h et de x, y, z dont tu ne donnes pas la signification ni rien, c'est pas clair du tout.
Bon, je me suis mal expliqué.
D'un point de vue géométrique la fonction f(x,y,z) représente un surface gauche.
En fait cette représentation géométrique n'existe que intellectuellement, mais c'est plus facile à imaginer.
En tout point de l'espace 3D à un couple de coordonnées (x,y) ou (x,z) ou (y,z), correspond de façon univoque la troisième coordonnée.
On pourrait peut-être écrire Surface = f(x, y, z), de même façon qu'on pourrait écrire dans le plan Droite = f(x, y)
Je me demande si on ne rejoint pas une discussion sur la différence entre linéaire et affine ?
J'ai vraiment besoin d'une remise à niveau.
D'un point de vue géométrique la fonction f(x,y,z) représente un surface gauche.
En fait cette représentation géométrique n'existe que intellectuellement, mais c'est plus facile à imaginer.
En tout point de l'espace 3D à un couple de coordonnées (x,y) ou (x,z) ou (y,z), correspond de façon univoque la troisième coordonnée.
On pourrait peut-être écrire Surface = f(x, y, z), de même façon qu'on pourrait écrire dans le plan Droite = f(x, y)
Je me demande si on ne rejoint pas une discussion sur la différence entre linéaire et affine ?
J'ai vraiment besoin d'une remise à niveau.
Skullkid a écrit:Le truc c'est que "la fonction f(x,y,z) représente une surface gauche" ça ne veut rien dire en soi, même en admettant l'abus de langage image = fonction. Ta surface tu la définis comment ? C'est l'ensemble des points (x,y,z) qui vérifient quoi ? f(x,y,z) = 0 ?
Une surface, qu'elle soit gauche ou pas, a une définition très claire.
Imaginons que cette surface soit plane, ce serait un plan.
Oui, il est vrai que l'on peut écrire f(x, y, z) =0.
Mais dans la pratique le but est naturellement de pouvoir écrire x=f(y, z) etc.
Dlzlogic a écrit:Une surface, qu'elle soit gauche ou pas, a une définition très claire.
Quelle est cette définition ? Et as-tu une définition de "la surface représentée par f" ?
Dlzlogic a écrit:Oui, il est vrai que l'on peut écrire f(x, y, z) =0.
Mais dans la pratique le but est naturellement de pouvoir écrire x=f(y, z) etc.
Donc tu as à ta disposition une fonction f, et tu cherches à décrire l'ensemble des points (x,y,z) qui annulent f comme étant par exemple l'ensemble des points (x,y,z) tels que x = g(y,z), c'est bien ça ? Quel est ton problème au final ?
Bonjour Skullkid,
Donc, je suis perdu.
J'ai l'impression qu'on fait un amalgame entre "savoir" et "comprendre", c'est pas parce qu'on comprend jusqu'à une étape à propos d'un sujet qu'on a une connaissance de la totalité du sujet, la logique démonstrative semble une notion oubliée. C'est tout ça mon problème.
Que je me fais régulièrement rappeler à l'ordre à propos de l'emploi de termes. Le terme "fonction" est le dernier en date, il y a eu l'emploi du signe '=' pour une valeur numérique, a contrario, j'ai dit qu'il n'existait pas de "valeur exacte" pour cos(pi/12) et on me répond que rac(2) ou rac(3) sont des valeurs exactes.Quel est ton problème au final ?
Donc, je suis perdu.
J'ai l'impression qu'on fait un amalgame entre "savoir" et "comprendre", c'est pas parce qu'on comprend jusqu'à une étape à propos d'un sujet qu'on a une connaissance de la totalité du sujet, la logique démonstrative semble une notion oubliée. C'est tout ça mon problème.
Dans ce cas il faut revoir la définition des termes que tu emploies. Il ne s'agit pas de savoir ou de comprendre. Chaque mot a un sens. Si tu utilises un mot sans connaître son sens, tu ne seras pas compris par les autres.
Pour ce qui est des fonctions, je pense que tu sais ce que c'est, c'est un machin qui mange un truc et qui en recrache un autre. Définir une fonction f ça revient à définir ce qu'elle mange et ce qu'elle recrache (mathématiquement parlant, il faut lui donner un ensemble de départ, un ensemble d'arrivée et un graphe), je ne vois toujours pas pourquoi tu as pris un exemple où tu parles de surfaces...
Si tu dis qu'il n'existe pas de valeur exacte pour cos(pi/12) tu as clairement faux, encore une fois ça n'a rien à voir avec des histoires de logique ou je ne sais quoi. cos(pi/12) c'est un réel en particulier, et pas un autre : c'est cos(pi/12). Il se trouve qu'en plus on en connaît une écriture simple qui n'utilise pas la fonction cos, mais peu importe.
Tu dis qu'on t'a repris parce que tu as utilisé le signe = pour une valeur numérique, c'est faux. Je sais que je t'ai repris une fois pour avoir utilisé le signe = dans le cadre d'une approximation. Tu confonds valeur numérique et valeur approchée, ça n'a rien à voir. Une valeur approchée n'est pas une valeur exacte, si tu écris en maths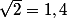 tu as faux, parce que
tu as faux, parce que  n'est pas égal à 1,4. Et quand, dans un cadre physique/ingénierie on écrit
n'est pas égal à 1,4. Et quand, dans un cadre physique/ingénierie on écrit 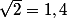 ou
ou 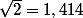 , le signe = ne traduit pas une égalité mathématique. Ce sont deux langues différentes, dans la langue mathématique le symbole = signifie "égalité", dans la langue physique il signifie "l'ordre de grandeur de la différence entre les deux membres est petit devant l'ordre de grandeur caractéristique du phénomène que j'étudie".
, le signe = ne traduit pas une égalité mathématique. Ce sont deux langues différentes, dans la langue mathématique le symbole = signifie "égalité", dans la langue physique il signifie "l'ordre de grandeur de la différence entre les deux membres est petit devant l'ordre de grandeur caractéristique du phénomène que j'étudie".
Pour ce qui est des fonctions, je pense que tu sais ce que c'est, c'est un machin qui mange un truc et qui en recrache un autre. Définir une fonction f ça revient à définir ce qu'elle mange et ce qu'elle recrache (mathématiquement parlant, il faut lui donner un ensemble de départ, un ensemble d'arrivée et un graphe), je ne vois toujours pas pourquoi tu as pris un exemple où tu parles de surfaces...
Si tu dis qu'il n'existe pas de valeur exacte pour cos(pi/12) tu as clairement faux, encore une fois ça n'a rien à voir avec des histoires de logique ou je ne sais quoi. cos(pi/12) c'est un réel en particulier, et pas un autre : c'est cos(pi/12). Il se trouve qu'en plus on en connaît une écriture simple qui n'utilise pas la fonction cos, mais peu importe.
Tu dis qu'on t'a repris parce que tu as utilisé le signe = pour une valeur numérique, c'est faux. Je sais que je t'ai repris une fois pour avoir utilisé le signe = dans le cadre d'une approximation. Tu confonds valeur numérique et valeur approchée, ça n'a rien à voir. Une valeur approchée n'est pas une valeur exacte, si tu écris en maths
C'est exactement le sens de ma question initiale.Dans ce cas il faut revoir la définition des termes que tu emploies.
Maintenant je sais que racine(2) "est" une valeur exacte, mais je ne sais toujours pas comment l'exprimer. Le développement en série ne me donnera toujours qu'une valeur approchée. Y aurait-il une autre méthode que je ne connais pas ?
Je viens d'apprendre aussi que les mathématiques et la physique suivent deux directions parallèles, c'est à dire se rencontrent rarement, moi qui croyais que l'un était l'antécédent de l'autre. :triste:
Dlzlogic a écrit:C'est exactement le sens de ma question initiale.
Maintenant je sais que racine(2) "est" une valeur exacte, mais je ne sais toujours pas comment l'exprimer. Le développement en série ne me donnera toujours qu'une valeur approchée. Y aurait-il une autre méthode que je ne connais pas ?
Mais
Dlzlogic a écrit:Je viens d'apprendre aussi que les mathématiques et la physique suivent deux directions parallèles, c'est à dire se rencontrent rarement, moi qui croyais que l'un était l'antécédent de l'autre. :triste:
Je n'ai pas dit ça, j'ai dit qu'elles parlaient deux langages différents. Ces deux langages sont très liés, mais ils sont quand même différents. Le symbole = ne veut pas dire la même chose, les objets du genre dx ne veulent pas non plus dire la même chose, etc. Quant à savoir qui était là avant l'autre c'est une question de point de vue et je ne rentrerai pas dans le débat.
Billball a écrit:sinon tu mets : f = f(x,y,z) là ca parait clair..
Oui, ça revient à utiliser l'abus de langage "image = fonction" dont j'ai parlé plus tôt, mais je dois dire que j'ai toujours pas compris ce qui bloquait Dlzlogic au niveau des fonctions...
Je suis aussi curieux de voir la définition "très claire" (et je l'espère, très satisfaisante) d'une surface...
Bonjour,
Concernant le sens du terme "fonction"
1ère hypothèse : une fonction est une relation telle qu'à gauche du signe "=" il y a une valeur, et à droite une expression contenant une ou plusieurs variables et constantes qui permet de calculer cette valeur. Ce sera une fonction univoque.
2nd hypothèse : une fonction est une relations entre plusieurs variables et constantes, telle que la connaissance d'une valeur de chacune des variables, sauf une, permet généralement de déterminer celle-ci.
Dans la première hypothèse, la parabole à axe vertical sera la courbe représentative d'une fonction, mais pas le cercle, et en particulier pas le colimaçon et pas la clothoïde.
Dans la seconde hypothèse ces "courbes exclues" seront aussi représentatives de fonctions.
La définition d'une surface est très simple : une surface divise l'espace 3D en deux ensembles, de la même façon qu'une ligne continue et non limitée divise le plan en 2 ensembles.
Je me permettrais de revenir sue quelque points :
1- le signe égal.
Il est employé en math et en physique avec la même signification.
S'il s'agit d'égalité de valeurs dénombrables, il n'y a pas d'ambiguïté (nombre de boules dans une urne utilisé pour l'apprentissage de l'analyse combinatoire).
Lorsqu'il s'agit de valeurs réelles, elle ne sont pas dénombrables. En math, on ne sait pas trop comment le noter, alors, on dit "à peu près" ou "à 10^3" près ou je ne sais quoi.
En physique, on sait que une quantité de choses n'ont pas de valeur exacte, une longueur, une surface, un volume, une vitesse, une intensité électrique etc. Alors on sait très bien ce qu'il faut faire : le nombre de chiffres écrits, généralement après la virgule, indique la précision donnée.
Si je dis que cette longueur mesure 10.25 m. cela signifie que cette valeur numérique indique que la valeur réelle est comprise entre 10.245 et 10.255. Mais il n'est nullement exclu qu'il y ai eu une erreur (à distinguer soigneusement de "faute") et que la "valeur vraie' est 10.2184. Ces notions ont été détaillées dans un autre sujet.
2- la notation racine(2).
C'est une notation, strictement équivalente à 2^1/2. C'est une notation simple, utile pour les valeurs 2, 3, 5 qui sont d'ailleurs celles que chacun connait par cur, mais ce ne sont que des notations. La valeur qu'elles représentent n'a rien d'exact.
3- le rapport entre les mathématiques et la physique (et d'autres sciences qui ont les mêmes caractéristiques)
Sans la physique, les mathématiques n'auraient aucune raison d'être, de même que l'informatique s'il n'y avait pas les applications. (petit parallèle pour les lecteurs assidus avec les liens entre les probabilités et les statistiques).
PS. La langue française me parait suffisamment précise pou éviter des termes comme "truc" ou des termes gastriques.
Concernant le sens du terme "fonction"
1ère hypothèse : une fonction est une relation telle qu'à gauche du signe "=" il y a une valeur, et à droite une expression contenant une ou plusieurs variables et constantes qui permet de calculer cette valeur. Ce sera une fonction univoque.
2nd hypothèse : une fonction est une relations entre plusieurs variables et constantes, telle que la connaissance d'une valeur de chacune des variables, sauf une, permet généralement de déterminer celle-ci.
Dans la première hypothèse, la parabole à axe vertical sera la courbe représentative d'une fonction, mais pas le cercle, et en particulier pas le colimaçon et pas la clothoïde.
Dans la seconde hypothèse ces "courbes exclues" seront aussi représentatives de fonctions.
La définition d'une surface est très simple : une surface divise l'espace 3D en deux ensembles, de la même façon qu'une ligne continue et non limitée divise le plan en 2 ensembles.
Je me permettrais de revenir sue quelque points :
1- le signe égal.
Il est employé en math et en physique avec la même signification.
S'il s'agit d'égalité de valeurs dénombrables, il n'y a pas d'ambiguïté (nombre de boules dans une urne utilisé pour l'apprentissage de l'analyse combinatoire).
Lorsqu'il s'agit de valeurs réelles, elle ne sont pas dénombrables. En math, on ne sait pas trop comment le noter, alors, on dit "à peu près" ou "à 10^3" près ou je ne sais quoi.
En physique, on sait que une quantité de choses n'ont pas de valeur exacte, une longueur, une surface, un volume, une vitesse, une intensité électrique etc. Alors on sait très bien ce qu'il faut faire : le nombre de chiffres écrits, généralement après la virgule, indique la précision donnée.
Si je dis que cette longueur mesure 10.25 m. cela signifie que cette valeur numérique indique que la valeur réelle est comprise entre 10.245 et 10.255. Mais il n'est nullement exclu qu'il y ai eu une erreur (à distinguer soigneusement de "faute") et que la "valeur vraie' est 10.2184. Ces notions ont été détaillées dans un autre sujet.
2- la notation racine(2).
C'est une notation, strictement équivalente à 2^1/2. C'est une notation simple, utile pour les valeurs 2, 3, 5 qui sont d'ailleurs celles que chacun connait par cur, mais ce ne sont que des notations. La valeur qu'elles représentent n'a rien d'exact.
3- le rapport entre les mathématiques et la physique (et d'autres sciences qui ont les mêmes caractéristiques)
Sans la physique, les mathématiques n'auraient aucune raison d'être, de même que l'informatique s'il n'y avait pas les applications. (petit parallèle pour les lecteurs assidus avec les liens entre les probabilités et les statistiques).
PS. La langue française me parait suffisamment précise pou éviter des termes comme "truc" ou des termes gastriques.
Dlzlogic a écrit:Bonjour,
Concernant le sens du terme "fonction"
1ère hypothèse : une fonction est une relation telle qu'à gauche du signe "=" il y a une valeur, et à droite une expression contenant une ou plusieurs variables et constantes qui permet de calculer cette valeur. Ce sera une fonction univoque.
2nd hypothèse : une fonction est une relations entre plusieurs variables et constantes, telle que la connaissance d'une valeur de chacune des variables, sauf une, permet généralement de déterminer celle-ci.
La langue française est surement bien fournie, mais au moins la définition avec "truc" de skullkid a le mérite d'être clair contrairement aux deux ci dessus qui n'ont pas grand sens.
Une fonction, formellement, est une relation entre deux ensembles de sorte qu'un élément au départ ne peut être mis en relation qu'avec au plus un élément à l'arrivée.
Avec cette définition, les cercles et cie. ne sont pas des fonctions.
2- la notation racine(2).
C'est une notation, strictement équivalente à 2^1/2. C'est une notation simple, utile pour les valeurs 2, 3, 5 qui sont d'ailleurs celles que chacun connait par cur, mais ce ne sont que des notations. La valeur qu'elles représentent n'a rien d'exact.
Tout comme 3 est une notation qui désigne le troisième nombre entier. Donc en suivant ton raisonnement, 3 n'a rien d'exact non plus!
Sinon, pour le signe "=", qu'est-ce que tu appelles des "valeurs dénombrables"?
Bonjour Nightmare.
Bon, maintenant c'est clair, concernant la définition d'une fonction, c'est la première hypothèse, même si ma formulation n'était pas claire.
Il me semble que l'on travaille avec des ensembles définis, les entiers, les réels, les complexes.
Le chiffre 3 est défini dans l'ensemble des entiers. Chaque élément de cet ensemble est exact par définition 3 = 2 +1 ; 3 = 4 -1 .
Cet ensemble possède un certain nombre de caractéristiques (opérateurs, élément neutre, invariant etc). Le signe "racine nième de ..." ne correspond à aucune de ces caractéristiques. C'est un élément typographique pour exprimer la puissance de 1 sur n.
Si aucun chiffre n'est précisé dans le V du symbole, c'est le 2 qui est sous-entendu.
Dans un domaine de définition donné, j'appelle "valeur dénombrable" une valeur V telle que on puisse trouver une valeur V1 telle que V1 = V + e.
On peut l'exprimer autrement, si min et max sont les bornes du domaine de définition, le nombre de ses éléments est (max - min).
Ceci est vrai pour les entiers, mais faux pour les réels. Dans certaines applications, l'informatique en particulier, la méconnaissance de cela a des conséquences désagréables.
Bon, maintenant c'est clair, concernant la définition d'une fonction, c'est la première hypothèse, même si ma formulation n'était pas claire.
Il me semble que l'on travaille avec des ensembles définis, les entiers, les réels, les complexes.
Le chiffre 3 est défini dans l'ensemble des entiers. Chaque élément de cet ensemble est exact par définition 3 = 2 +1 ; 3 = 4 -1 .
Cet ensemble possède un certain nombre de caractéristiques (opérateurs, élément neutre, invariant etc). Le signe "racine nième de ..." ne correspond à aucune de ces caractéristiques. C'est un élément typographique pour exprimer la puissance de 1 sur n.
Si aucun chiffre n'est précisé dans le V du symbole, c'est le 2 qui est sous-entendu.
Dans un domaine de définition donné, j'appelle "valeur dénombrable" une valeur V telle que on puisse trouver une valeur V1 telle que V1 = V + e.
On peut l'exprimer autrement, si min et max sont les bornes du domaine de définition, le nombre de ses éléments est (max - min).
Ceci est vrai pour les entiers, mais faux pour les réels. Dans certaines applications, l'informatique en particulier, la méconnaissance de cela a des conséquences désagréables.
Salut Dlzlogic, je vais pas te cacher que c'est franchement peu clair ce que tu racontes, et la principale raison est que tu expliques des mots en en employant d'autres qui sont pas forcément plus clairs que ceux que tu essayes d'expliquer...
Qu'est-ce que tu appelles défini? Ab contrario, qu'est-ce que tu appellerais un ensemble indéfini ?
Qu'entends-tu par "défini dans les entiers" et par "exact" ?
Que'appelles-tu "caractéristiques", parce que dans ton etc. on peut mettre tout et n'importe quoi...
A priori, tout comme 2 est un élément typographique pour désigner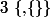 dans la définition des entiers naturels par la théorie des ensembles.
dans la définition des entiers naturels par la théorie des ensembles.
Ensuite, concernant dénombrable, c'est pas clair non plus.
Qui est V1 ? Qui est e? A priori, de telles valeurs existent aussi toujours chez les réels.
Concernant le min et le max, si je prends l'ensemble d'entiers {2,4,6} alors max - min=4 qui n'est pas égal au nombre de ses éléments...
Il me semble que l'on travaille avec des ensembles définis, les entiers, les réels, les complexes.
Qu'est-ce que tu appelles défini? Ab contrario, qu'est-ce que tu appellerais un ensemble indéfini ?
Le chiffre 3 est défini dans l'ensemble des entiers. Chaque élément de cet ensemble est exact par définition 3 = 2 +1 ; 3 = 4 -1 .
Qu'entends-tu par "défini dans les entiers" et par "exact" ?
Cet ensemble possède un certain nombre de caractéristiques (opérateurs, élément neutre, invariant etc). Le signe "racine nième de ..." ne correspond à aucune de ces caractéristiques.
Que'appelles-tu "caractéristiques", parce que dans ton etc. on peut mettre tout et n'importe quoi...
C'est un élément typographique pour exprimer la puissance de 1 sur n.
A priori, tout comme 2 est un élément typographique pour désigner
Ensuite, concernant dénombrable, c'est pas clair non plus.
Qui est V1 ? Qui est e? A priori, de telles valeurs existent aussi toujours chez les réels.
Concernant le min et le max, si je prends l'ensemble d'entiers {2,4,6} alors max - min=4 qui n'est pas égal au nombre de ses éléments...
Les nombres réels, c'est aussi un truc bien défini
On peut prendre une définition abstraite, comme "R est l'unique corps totalement ordonné qui satisfait l'axiome de la borne supérieure".
Ou alors on peut en donner une construction explicite : [url]http://fr.wikipedia.org/wiki/Construction_des_nombres_réels[/url]
Quand on parle d'un réel, on a quasiment toujours (à moins de le faire vraiment exprès) un algorithme pour calculer une suite d'approximations rationnelles qui converge vers ce réel. Donc si on a assez de temps de calcul, on pourra toujours donner des approximations aussi précises que l'on veut.
Si on a deux nombres réels distincts, on peut alors voir en temps fini qu'ils sont distincts en prenant des approximations suffisemment précises.
(par contre on ne peut pas montrer que deux réels sont égaux seulement en regardant des suites qui les approximent)
Par exemple pour sqrt(2), le théorème des valeurs intermédiaires dit qu'il existe un réel x entre 1 et 2 tel que x²= 2. Ce théorème calcule une suite d'approximations par dichotomie qui converge vers sqrt(2) : 3/2 +-1/2, 5/4 +-1/4, 11/8 +- 1/8, 23/16 +-1/16, 45/32, 91/64 ..., et cette suite définit le réel sqrt(2).
Quand dans un énoncé on demande de calculer "une valeur exacte", en général ça veut dire "mettre le nombre réel sous la forme d'une expression la plus simple possible"
On peut prendre une définition abstraite, comme "R est l'unique corps totalement ordonné qui satisfait l'axiome de la borne supérieure".
Ou alors on peut en donner une construction explicite : [url]http://fr.wikipedia.org/wiki/Construction_des_nombres_réels[/url]
Quand on parle d'un réel, on a quasiment toujours (à moins de le faire vraiment exprès) un algorithme pour calculer une suite d'approximations rationnelles qui converge vers ce réel. Donc si on a assez de temps de calcul, on pourra toujours donner des approximations aussi précises que l'on veut.
Si on a deux nombres réels distincts, on peut alors voir en temps fini qu'ils sont distincts en prenant des approximations suffisemment précises.
(par contre on ne peut pas montrer que deux réels sont égaux seulement en regardant des suites qui les approximent)
Par exemple pour sqrt(2), le théorème des valeurs intermédiaires dit qu'il existe un réel x entre 1 et 2 tel que x²= 2. Ce théorème calcule une suite d'approximations par dichotomie qui converge vers sqrt(2) : 3/2 +-1/2, 5/4 +-1/4, 11/8 +- 1/8, 23/16 +-1/16, 45/32, 91/64 ..., et cette suite définit le réel sqrt(2).
Quand dans un énoncé on demande de calculer "une valeur exacte", en général ça veut dire "mettre le nombre réel sous la forme d'une expression la plus simple possible"
Pardon pour l'emploi du terme "défini", j'aurais dû dire précisé ou connu ou fixé.
Concernant les problèmes relatifs à la différenciation entiers-réels, dénombrables-non dénombrables, en théorie et sur le papier, vous avez certainement raison, mais concernant leur utilisation, je pense à l'informatique, apparemment vous n'avez jamais été confrontés à ce problème.
Wiki ne constituera jamais une référence pour quiconque.
Donc, je retire tout ce que j'ai dit, et j'ai bien pris note que "exact" signifie "mettre le nombre réel sous la forme d'une expression la plus simple possible".
Concernant les problèmes relatifs à la différenciation entiers-réels, dénombrables-non dénombrables, en théorie et sur le papier, vous avez certainement raison, mais concernant leur utilisation, je pense à l'informatique, apparemment vous n'avez jamais été confrontés à ce problème.
Wiki ne constituera jamais une référence pour quiconque.
Donc, je retire tout ce que j'ai dit, et j'ai bien pris note que "exact" signifie "mettre le nombre réel sous la forme d'une expression la plus simple possible".
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
