Tiens, j'ai trouvé un petit exercice sympa regroupant plusieurs notions vues précédemment.
Partie ISoit
\in\mathbb{R}^2)
. On considère
}= \begin{pmatrix} a+b & -b \\ b & a \end{matrix})
.
Soit

l'ensemble des matrices telles que
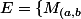}\ |\ (a,b)\in\mathbb{R}^2\})
.
On rappelle que
)
est un anneau commutatif unitaire.
1°) Montrer que

est une partie de
,+ \))
et de
,\times \))
.
2°) Montrer que
)
est un anneau unitaire commutatif.
3°)a) Montrer que pour tous réels

:
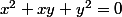
équivaut à
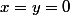
.
3°)b) Déterminer les éléments inversibles de

.
c) En déduire que
)
est un corps commutatif.
Partie IISoit

un nombre complexe non réel.
1°) Montrer que
)
est une base de l'espace vectoriel réel
)
.
2°) On considère l'application

qui, à toute matrice
})
, associe le complexe

.
Montrer que \psi est un morphisme bijectif de
)
vers
)
.
3°) Résoudre dans

l'équation

.
Donner les solutions sous forme trigonométrique.
4°) On suppose dans cette question que
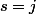
.
Montrer que \psi est un morphisme de
)
vers
)
.
Partie I. Soit
}, M_{(a',b')}\in M_2\(\mathbb{R} \))
.
J'ai montré que
}+M_{(a',b')}=M_{(a+a',b+b')} \in E)
et
}\times M_{(a',b')}=M_{(aa'-bb',ab'+a' b +bb' )}\in E)
.
D'où la conclusion.
2°) Ici j'ai pensé à montrer que

est un sous-anneau de
,+,\times \))
, mais je ne sais plus comment faire.
3°)a) Ici deux manières me sont venues à l'esprit.
1re méthode : Pour tous réels

:
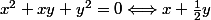^2 + \frac{3}{4} y^2=0)
.
Or
^2 \ge 0)
et

donc
^2 + \frac{3}{4} y^2=0\Longleftrightarrow \( x+ \frac{1}{2} y \)^2 = \frac{3}{4} y^2=0 \Longleftrightarrow x=y=0)
.
2e méthode : Fixons

. Résolvons alors l'équation, de paramètre réel

:

.

.
- Si

alors l'équation admet une racine double

;
- Si
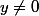
alors
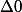
.
De plus, quels que soient les réels

:

donc par symétrie des rôles, on en déduis que
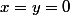
.
b)
})
est inversible si et seulement si
} \)\neq 0)
i.e.

, donc si et seulement si
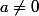
et
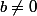
.
Donc l'ensemble des matrices de

inversibles est
} \})
.
Par contre, je ne vois pas comment trouver
}^{-1})
.
