Hello,
le principe de la démo de Lagrange que tu as faite est très simple :
On décompose le groupe G de la manière suivante :
On prend un élément

quelconque dans G et on effectue tous les produits

possible où h décrit H. Il y en autant que d'éléments dans H.
Ca nous donne une première classe
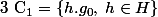
qui a card(H) éléments.
Parmi les éléments restants dans G, c'est à dire ceux qui ne sont pas de la forme h.g0, on en choisit un quelconque

, et de même on effectue tous les produits

avec h décrivant H. On obtient une deuxième classe
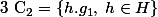
qui a aussi card(H) éléments.
On réitère en prenant un élément g2 que l'on a pas encore rencontré dans les calculs précédents et caetera jusqu'à épuisement des éléments de G.
Au final, on aura décomposé G en un certain nombre de classes qui ont toutes le cardinal de H. On obtient bien alors que card(G) est un multiple de card(H) et que le quotient est le nombre de classes construites précédemment.
De façon symbolique :
Avec p=card(H) :
=k\times p)
au début ?
