Groupes - morphismes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Juil 2012, 10:45
par capitaine nuggets » 25 Juil 2012, 10:45
D'accord.
Je m'attaque maintenant à un grand classique, du moins je crois :
Montrer que tous les sous-groupes de
)
sont de la forme
)
avec

.
Mais je ne vois pas comment y parvenir :triste:
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 25 Juil 2012, 12:16
par vincentroumezy » 25 Juil 2012, 12:16
capitaine nuggets a écrit:D'accord.
Je m'attaque maintenant à un grand classique, du moins je crois :
Montrer que tous les sous-groupes de
)
sont de la forme
)
avec

.
Mais je ne vois pas comment y parvenir :triste:
Ah oui, grand classique !
Montres d'abord que tous les
)
sont des sous-groupes de Z.
Ensuite, prends H un sg de Z (différent de {0} et Z), et montres qu'il est de la forme nZ

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 26 Juil 2012, 00:25
par capitaine nuggets » 26 Juil 2012, 00:25
vincentroumezy a écrit:Ah oui, grand classique !
Montres d'abord que tous les
)
sont des sous-groupes de Z.
Ensuite, prends H un sg de Z (différent de {0} et Z), et montres qu'il est de la forme nZ
Ok :++:
-

;
- Soient

.
Dans ce cas, il existe

tels que

et
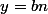
donc
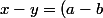n\in n\mathbb{Z})
.
Donc tous les groupes
)
sont des sous-groupes du groupe
)
.
Par contre, je n'y arrive pas

-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 26 Juil 2012, 10:36
par vincentroumezy » 26 Juil 2012, 10:36
Soit H un sous groupe de

, si H={0}, alors H=0Z, ok. Si H=Z, alors H=1*Z, ok.
Si H n'est ni {0} ni Z. Prenons n le plus élément strictement positif de H (il existe)
Montrons alors que H=nZ par double inclusion (nZ inclus dans H est simple, l'autre est plus ardue).

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 26 Juil 2012, 21:28
par capitaine nuggets » 26 Juil 2012, 21:28
Nam vraiment je ne vois pas bien comment faire.
C'est assez obscur pour moi.
Puis d'ailleurs, je ne vois pas pourquoi, il faudrait montrer ça.
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 26 Juil 2012, 22:00
par vincentroumezy » 26 Juil 2012, 22:00
Si tu prends un sous groupe quelconque de Z et que tu montres qu'il est de la forme nZ, tu as bien réussi, non ?
Il existe (i,j) j positif, jor j est positif et strictement inférieur à n, donc j=0, donc x=in, donc H=nZ.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 27 Juil 2012, 03:49
par capitaine nuggets » 27 Juil 2012, 03:49
vincentroumezy a écrit:Si tu prends un sous groupe quelconque de Z et que tu montres qu'il est de la forme nZ, tu as bien réussi, non ?
Oui.
vincentroumezy a écrit:Il existe (i,j) j positif, j<n tels que x=in+j. Quelque soit le signe de i, in appartient à H, donc j=x-in appartient à H.
or j est positif et strictement inférieur à n, donc j=0, donc x=in, donc H=nZ.
Là je comprends pas pourquoi tu sors un "il existe (i,j)".
Qu'est-ce que x ?
Cette partie-là sert à montrer quoi ?
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 27 Juil 2012, 08:49
par vincentroumezy » 27 Juil 2012, 08:49
capitaine nuggets a écrit:Oui.
Là je comprends pas pourquoi tu sors un "il existe (i,j)".
Qu'est-ce que x ?
Cette partie-là sert à montrer quoi ?
Le couple (i,j) c'est simplement une division euclidienne.
J'ai oublié de définir x, c'est un élément quelconque de H.
Regarde la conclusion, qu'a t'on démontré ?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 27 Juil 2012, 09:01
par capitaine nuggets » 27 Juil 2012, 09:01
Alors si j'ai bien compris :
1re étape : on vérifie que tous les nZ sont des sous-groupes de Z ;
2e étape : on montre qu'un sous-groupes de Z est de la forme nZ ;
3e étape : on montre que tout les sous-groupes sont nZ.
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 27 Juil 2012, 09:21
par vincentroumezy » 27 Juil 2012, 09:21
capitaine nuggets a écrit:Alors si j'ai bien compris :
1re étape : on vérifie que tous les nZ sont des sous-groupes de Z ;
2e étape : on montre qu'un sous-groupes de Z est de la forme nZ ;
3e étape : on montre que tout les sous-groupes sont nZ.
Pas vraiment, à l'étape 2 on montre que tous ( puisque H est quelconque) les sg de Z sont des nZ, ce qui rend inutile l'étape 3.
En fait, c'est une doublie inclusion pour montrer que l'ensemble des sous groupes de Z est l'ensemble des nZ (on prend un nZ on montre que c'est un sg de Z, et réciproquement, on prend un sg de Z et on montre que c'est un nZ).

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 27 Juil 2012, 18:43
par capitaine nuggets » 27 Juil 2012, 18:43
vincentroumezy a écrit:En fait, c'est une doublie inclusion pour montrer que l'ensemble des sous groupes de Z est l'ensemble des nZ (on prend un nZ on montre que c'est un sg de Z, et réciproquement, on prend un sg de Z et on montre que c'est un nZ).
Ah ok, je comprends mieux :we:

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 28 Juil 2012, 14:13
par capitaine nuggets » 28 Juil 2012, 14:13
Bonjour !
J'aimerais à présent montrer que l'application
 \to (\mathbb{C},+,\times ))
est un isomorphisme de corps.
Pour cela, je veux montrer que c'est un morphisme pour l'addition et la multiplication et que l'application

est bijective.
Soient

tels que
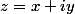
et
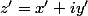
.
=f(x+x'+i(y+y'))=x+x'-i(y+y')=x-iy+x'-iy'=\bar z + \bar {z'}=f(z)+f(z'))
;
=f((x+iy)(x'+iy'))=f(xx'-yy'+i(xy'+yx'))=xx'-yy'-i(xy'+yx'))
et
\times f(z')= (x-iy)\times (x'-iy')=xx'+yy'-i(xy'+yx'))
donc
=f(z)\times f(z'))
;
Supposons que
=f(z'))
, montrons qu'alors
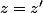
.
=f(z'))
équivaut à
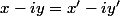
équivaut à
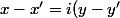)
.
Si
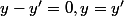
alors
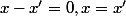
et donc
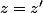
;
Si

alors
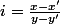
donc

ce qui est impossible.
Par conséquent,

est injective.
PAr contre, je n'arrive pas à montrer la surjectivité :triste:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Juil 2012, 14:21
par Doraki » 28 Juil 2012, 14:21
f(z) = z^12-35 ?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 28 Juil 2012, 14:51
par capitaine nuggets » 28 Juil 2012, 14:51
Doraki a écrit:f(z) = z^12-35 ?
Oups oui, j'ai oublié de préciser que
=\bar z)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Juil 2012, 15:06
par Doraki » 28 Juil 2012, 15:06
ok, donc pour la surjectivité, pour tout x et y réels, tu cherches deux réels a et b tels que a-ib = x+iy ?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 28 Juil 2012, 15:20
par capitaine nuggets » 28 Juil 2012, 15:20
Doraki a écrit:ok, donc pour la surjectivité, pour tout x et y réels, tu cherches deux réels a et b tels que a-ib = x+iy ?
Oui je suis d'accord, mais je n'arrive pas à avancer.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Juil 2012, 15:49
par Doraki » 28 Juil 2012, 15:49
que penses-tu de prendre a=x et b= -y ?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 28 Juil 2012, 15:55
par capitaine nuggets » 28 Juil 2012, 15:55
Doraki a écrit:que penses-tu de prendre a=x et b= -y ?
En fait, je dois t'avouer que je suis un peu confus.
D'habitude, les fonctions que je traite sont de R dans R donc c'est plus facile (en général) parce que j'ai l'habitude mais là...
Tu pourrais me développer ton idée stp ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Juil 2012, 16:38
par Doraki » 28 Juil 2012, 16:38
ben par exemple, le nombre complexe dont le conjugué est 27+14i, c'est 27-14i.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 28 Juil 2012, 17:19
par capitaine nuggets » 28 Juil 2012, 17:19
Ah oui, en fait c'est comme si on prenais une fonction de

dans

où, à tout couple
)
on associe
)
.
Du coup, si on pose
=g(x,y))
alors
=(x,-y))
donc
=(a,-b))
.
On a par conséquent, montré que, pour tout couple de réels
)
, il existe un couple de réels
)
tels que
=g(x,y))
. D'où

est injective.
--> Est-ce que
)
et
))
sont deux écritures de sens différents ?
--> Peut-on dire que les fonctions

et

définies par :
=\bar z)
et
=(x,-y))
,
sont isomorphes ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
sont de la forme
avec
.
sont des sous-groupes de Z.