Séries numériques
19 messages
- Page 1 sur 1
Séries numériques
Bonjour,
Pour étudier la nature d'une série numérique il suffit de calculer la limite de sa somme Un en 0 et à l'inifini (c'est juste) ?
j'ai la somme de (n+1)/(2n+1)
je dois étudier sa nature et calculer la somme en cas de convergence.Help
Merci
Pour étudier la nature d'une série numérique il suffit de calculer la limite de sa somme Un en 0 et à l'inifini (c'est juste) ?
j'ai la somme de (n+1)/(2n+1)
je dois étudier sa nature et calculer la somme en cas de convergence.Help
Merci
M. Ben314 m'a fait une remarque au sujet des limites des sommes:
"Quand tu as la somme de N éléments, la première chose qui doit venir à l'esprit, c'est de majorer par N * Le_plus_grand et de minorer par N * Le_plus_petit ..."
Par exemple, la somme citée dans votre exercice: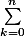
 ,
,
on aura (n+1)*

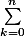

 (n+1)*
(n+1)* = n+1
= n+1 
^2}{2n+1})

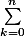

 n+1,
n+1,
donc en passant aux limites, vous pouvez facilement conclure.
"Quand tu as la somme de N éléments, la première chose qui doit venir à l'esprit, c'est de majorer par N * Le_plus_grand et de minorer par N * Le_plus_petit ..."
Par exemple, la somme citée dans votre exercice:
on aura (n+1)*
donc en passant aux limites, vous pouvez facilement conclure.
bonjour est-ce vous pouvez svp posté la correction de ces ex
[quote="loulou16"]Voici l'exercice. [img][IMG]http://img11.hostingpics.net/pics/841280image952.jpg[/img][/IMG][/QUOTE bonjour est-ce vous pouvez svp posté la correction de ces exercices
comme indique précédemment lors que tu cherches a savoir si une série converge le premier reflexe c'est de chercher la limite (ou un équivalent) du terme général
https://fr.wikipedia.org/wiki/S%C3%A9rie_convergente
https://fr.wikipedia.org/wiki/S%C3%A9rie_convergente
arnaud32 a écrit:comme indique précédemment lors que tu cherches a savoir si une série converge le premier reflexe c'est de chercher la limite (ou un équivalent) du terme général
https://fr.wikipedia.org/wiki/S%C3%A9rie_convergente
Ok mercii je vais m y lancer. Je bloque également sur ça n/(n+1)!
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
