Polynomes irréductibles dans C[x,y]
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 20 Mai 2007, 13:41
par Daniel-Jackson » 20 Mai 2007, 13:41
Rafar a écrit:Il me semble me rappeler que si P est dans
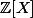
et que
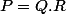
avec Q et R dans
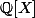
alors
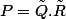
où
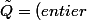.Q)
et
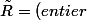.R)
avec
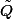
et
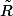
polynômes de
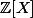
Quelqu'un peut-il confirmer ou infirmer SVP ? :help: (dans mon souvenir, il y a une histoire de contenant et un lemme de Gauss sur les contenants à montrer)
Je crois que tu t'es légèrement trompé .
Si Q est dans Q
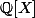
, pour faire apparaitre un polynome
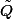
de
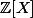
, il faut mettre en facteur l'inverse du ppcm des dénominateur des coefficients , donc on aura plutot :
}) ppcm(coeff Q).Q)
On note alors
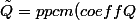.Q)
et pareit pour R...
Donc au final tu te retrouve avec un coefficient rationnel en tête des deux polynôme de Z[X]
-
Rafar
- Membre Naturel
- Messages: 37
- Enregistré le: 19 Mai 2007, 20:47
-
 par Rafar » 20 Mai 2007, 13:55
par Rafar » 20 Mai 2007, 13:55
Daniel-Jackson a écrit:Je crois que tu t'es légèrement trompé .
C'est bien possible ! :briques:
-
Emilie62
- Membre Naturel
- Messages: 51
- Enregistré le: 19 Mai 2007, 20:33
-
 par Emilie62 » 20 Mai 2007, 13:57
par Emilie62 » 20 Mai 2007, 13:57
Un doute ..... Tous les polynomes de
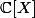
de degré supérieur ou égal à 2 sont réductibles ????
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 20 Mai 2007, 14:15
par Daniel-Jackson » 20 Mai 2007, 14:15
Emilie62 a écrit:Un doute ..... Tous les polynomes de
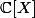
de degré supérieur ou égal à 2 sont réductibles ????
Oui
Tout polynome non constant admet au moins une racine : D'Alembert Gauss : C est algébriquement clos.
Les seuls irréductibles sont les polynomes de dégré inférieur ou égal à 1 (non nuls)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
et que
avec Q et R dans
alors
où
et
avec
et
polynômes de
